题目内容
 在平面直角坐标系xOy中,将从点M出发沿纵、横方向到达点N的任一路径称为M到N的一条“折线路径”,所有“折线路径”中长度最小的称为M到N的“折线距离”.如图所示的路径MD1D2D3N与路径MEN都是M到N的“折线路径”.某地有三个居民区分别位于平面xOy内三点A(-8,1),B(5,2),C(1,14),现计划在这个平面上某一点P(x,y)处修建一个超市.
在平面直角坐标系xOy中,将从点M出发沿纵、横方向到达点N的任一路径称为M到N的一条“折线路径”,所有“折线路径”中长度最小的称为M到N的“折线距离”.如图所示的路径MD1D2D3N与路径MEN都是M到N的“折线路径”.某地有三个居民区分别位于平面xOy内三点A(-8,1),B(5,2),C(1,14),现计划在这个平面上某一点P(x,y)处修建一个超市.(1)请写出点P到居民区A的“折线距离”d的表达式(用x,y表示,不要求证明);
(2)为了方便居民,请确定点P的位置,使其到三个居民区的“折线距离”之和最小.
考点:根据实际问题选择函数类型
专题:应用题,函数的性质及应用
分析:(1)根据“折线距离”的定义,可得点P到居民区A的“折线距离”长度最小值;
(II)由题意知,点P到三个居民区的“折线距离”长度之和的最小值为点P到三个居民区的“折线距离”长度最小值之和(记为d)的最小值,分类讨论,利用绝对值的几何意义,即可求得点P的坐标.
(II)由题意知,点P到三个居民区的“折线距离”长度之和的最小值为点P到三个居民区的“折线距离”长度最小值之和(记为d)的最小值,分类讨论,利用绝对值的几何意义,即可求得点P的坐标.
解答:
解:设点P的坐标为(x,y),则
(1)点P到居民区A的“折线距离”长度最小值为|x+8|+|y-1|,y∈[0,+∞);
(2)由题意知,点P到三个居民区的“折线距离”长度之和的最小值为点P到三个居民区的“折线距离”长度最小值之和(记为d)的最小值
∵d1(x)=|x+8|+|x-5|+|x-1|≥|x+8|+|x-5|≥13
∴当且仅当x=1时,d1(x)=|x+8|+|x-5|+|x-1|的最小值为13,
∵d2(y)=|y-1|+|y-2|+|y-14|≥|y-1|+|y-14|≥13
∴当且仅当y=2时,d2(y)=|y-1|+|y-2|+|y-14|的最小值为13
∴点P的坐标为(1,2)时,点P到三个居民区的“折线距离”长度之和的最小,且最小值为26.
(1)点P到居民区A的“折线距离”长度最小值为|x+8|+|y-1|,y∈[0,+∞);
(2)由题意知,点P到三个居民区的“折线距离”长度之和的最小值为点P到三个居民区的“折线距离”长度最小值之和(记为d)的最小值
∵d1(x)=|x+8|+|x-5|+|x-1|≥|x+8|+|x-5|≥13
∴当且仅当x=1时,d1(x)=|x+8|+|x-5|+|x-1|的最小值为13,
∵d2(y)=|y-1|+|y-2|+|y-14|≥|y-1|+|y-14|≥13
∴当且仅当y=2时,d2(y)=|y-1|+|y-2|+|y-14|的最小值为13
∴点P的坐标为(1,2)时,点P到三个居民区的“折线距离”长度之和的最小,且最小值为26.
点评:本题考查新定义,考查学生建模的能力,同时考查学生的理解能力,属于难题.

练习册系列答案
相关题目
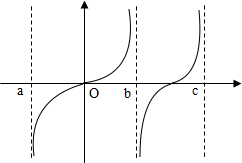 已知函数f(x),x∈(a,b)∪(b,c)的图象如图所示,有三个同学对此函数的单调性作出如下的判断:
已知函数f(x),x∈(a,b)∪(b,c)的图象如图所示,有三个同学对此函数的单调性作出如下的判断: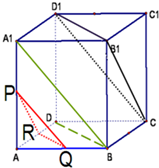 如图所示,已知正方体ABCD-A1B1C1D1中,P、Q、R分别为A1A、AB、AD的中点,求证:平面PQR∥平面CB1D1.
如图所示,已知正方体ABCD-A1B1C1D1中,P、Q、R分别为A1A、AB、AD的中点,求证:平面PQR∥平面CB1D1.