题目内容
平面内一动点P到点F(2,0)的距离比它到直线x+3=0的距离少1
(1)求动点P的轨迹方程;
(2)过点F(2,0)作一条倾斜角为α的直线,交抛物线于A(x1,y1),B(x2,y2)两点,线段AB的中点是M,直线OM的斜率kOM=f(α),求kOM=f(α)的取值范围.
(1)求动点P的轨迹方程;
(2)过点F(2,0)作一条倾斜角为α的直线,交抛物线于A(x1,y1),B(x2,y2)两点,线段AB的中点是M,直线OM的斜率kOM=f(α),求kOM=f(α)的取值范围.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线中的最值与范围问题
分析:(1)由抛物线定义可判断曲线为抛物线,从而可知p=2,得到方程;
(2)设直线AB:my=x-2,代入y2=8x,得y2-8my-16=0,利用韦达定理、中点坐标公式可表示M坐标,进而表示kOM=f(α),分m=0,m>0,m<0三种情况讨论,然后运用基本不等式可求斜率范围;
(2)设直线AB:my=x-2,代入y2=8x,得y2-8my-16=0,利用韦达定理、中点坐标公式可表示M坐标,进而表示kOM=f(α),分m=0,m>0,m<0三种情况讨论,然后运用基本不等式可求斜率范围;
解答:
解:(1)由题意知动点P的轨迹是以F为焦点、x=-2为准线的抛物线,
∴动点P的轨迹方程是y2=8x;
(2)设直线AB:my=x-2,代入y2=8x,得y2-8my-16=0,
则y1+y2=8m,y1y2=-16,
x1+x2=(my1+2)+(my2+2)=8m2+4,
∴M(4m2+2,4m),
∴kOM=f(α)=
=
,
当m=0时,kOM=0;
当m>0时,0<kOM=
≤
=
,当且仅当m=
时取等号;
当m<0时,0>kOM=
=
≥
=-
,当且仅当=-
时取等号;
综上所述,kOM=f(α)的取值范围是[-
,
].
∴动点P的轨迹方程是y2=8x;
(2)设直线AB:my=x-2,代入y2=8x,得y2-8my-16=0,
则y1+y2=8m,y1y2=-16,
x1+x2=(my1+2)+(my2+2)=8m2+4,
∴M(4m2+2,4m),
∴kOM=f(α)=
| 4m |
| 4m2+2 |
| 2m |
| 2m2+1 |
当m=0时,kOM=0;
当m>0时,0<kOM=
| 2 | ||
2m+
|
| 2 | ||||
2
|
| ||
| 2 |
| ||
| 2 |
当m<0时,0>kOM=
| 2 | ||
2m+
|
| -2 | ||
-2m-
|
| -2 | ||||
2
|
| ||
| 2 |
| ||
| 2 |
综上所述,kOM=f(α)的取值范围是[-
| ||
| 2 |
| ||
| 2 |
点评:该题考查抛物线的定义、方程及直线与抛物线的位置关系,考查斜率公式、基本不等式等知识,考查分类讨论思想.

练习册系列答案
相关题目
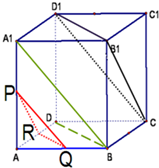 如图所示,已知正方体ABCD-A1B1C1D1中,P、Q、R分别为A1A、AB、AD的中点,求证:平面PQR∥平面CB1D1.
如图所示,已知正方体ABCD-A1B1C1D1中,P、Q、R分别为A1A、AB、AD的中点,求证:平面PQR∥平面CB1D1.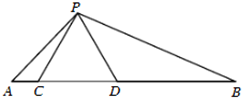 如图,点C、D在线段AB上,且△PCD是等边三角形.
如图,点C、D在线段AB上,且△PCD是等边三角形.