题目内容
已知椭圆E1:
+
=1(a>b>0)椭圆E2的中心在坐标原点,焦点在x轴上,其长轴长和短轴长分别是椭圆E1长轴长和短轴长的
倍(λ>0,λ≠1).
(Ⅰ)求椭圆E2的方程;并证明椭圆E1,E2的离心率相同;
(Ⅱ)当λ=2时,设M,N是椭圆E1上的两个点,OM,ON的斜率分别是kOM,kON,且kOM•kON=-
(O是坐标原点),若OMPN是平行四边形,证明:点P在椭圆E2上.
| x2 |
| a2 |
| y2 |
| b2 |
| λ |
(Ⅰ)求椭圆E2的方程;并证明椭圆E1,E2的离心率相同;
(Ⅱ)当λ=2时,设M,N是椭圆E1上的两个点,OM,ON的斜率分别是kOM,kON,且kOM•kON=-
| b2 |
| a2 |
考点:直线与圆锥曲线的关系,椭圆的标准方程,椭圆的简单性质
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)根据长轴长和短轴长分别是椭圆E1长轴长和短轴长的
倍,可得椭圆E2的方程;确定焦距长也为椭圆E1焦距长的
倍,即可证明椭圆E1,E2的离心率相同;
(Ⅱ)设M(acosα,bsinα),N(acosβ,bsinβ),则由kOM•kON=-
,可得cos(α-β)=0,确定P的坐标,代入椭圆E2的方程,即可得证.
| λ |
| λ |
(Ⅱ)设M(acosα,bsinα),N(acosβ,bsinβ),则由kOM•kON=-
| b2 |
| a2 |
解答:
(Ⅰ)解:设椭圆E1,E2的离心率分别为e1,e2,则
∵长轴长和短轴长分别是椭圆E1长轴长和短轴长的
倍,
∴椭圆E2的方程为
+
=1.
又长轴长和短轴长分别是椭圆E1长轴长和短轴长的
倍,
∴焦距长也为椭圆E1焦距长的
倍,
∴椭圆E1,E2的离心率相同;
(Ⅱ)证明:设M(acosα,bsinα),N(acosβ,bsinβ),则
∵kOM•kON=-
,
∴
tanα•
tanβ=-
,
∴tanα•tanβ=-1,
∴cos(α-β)=0.
设P(x,y),则∵OMPN是平行四边形,
∴x=a(cosα+cosβ),y=b(sinα+sinβ),
∴λ=2时,
+
=
[2+2cos(α-β)]=1,
∴点P在椭圆E2上.
∵长轴长和短轴长分别是椭圆E1长轴长和短轴长的
| λ |
∴椭圆E2的方程为
| x2 |
| λa2 |
| y2 |
| λb2 |
又长轴长和短轴长分别是椭圆E1长轴长和短轴长的
| λ |
∴焦距长也为椭圆E1焦距长的
| λ |
∴椭圆E1,E2的离心率相同;
(Ⅱ)证明:设M(acosα,bsinα),N(acosβ,bsinβ),则
∵kOM•kON=-
| b2 |
| a2 |
∴
| b |
| a |
| a |
| b |
| b2 |
| a2 |
∴tanα•tanβ=-1,
∴cos(α-β)=0.
设P(x,y),则∵OMPN是平行四边形,
∴x=a(cosα+cosβ),y=b(sinα+sinβ),
∴λ=2时,
| x2 |
| λa2 |
| y2 |
| λb2 |
| 1 |
| 2 |
∴点P在椭圆E2上.
点评:本题考查椭圆的方程,考查椭圆的参数方程,考查学生分析解决问题的能力,有难度.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
过点(-1,3)且平行于直线x-2y+3=0的直线方程为( )
| A、x-2y=0 |
| B、2x+y-1=0 |
| C、x-2y+7=0 |
| D、2x+y-5=0 |
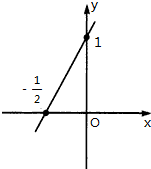 已知二次函数f(x)=ax2+bx+c(c>0且为常数)的导函数的图象如图.
已知二次函数f(x)=ax2+bx+c(c>0且为常数)的导函数的图象如图.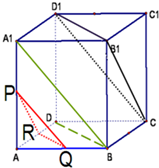 如图所示,已知正方体ABCD-A1B1C1D1中,P、Q、R分别为A1A、AB、AD的中点,求证:平面PQR∥平面CB1D1.
如图所示,已知正方体ABCD-A1B1C1D1中,P、Q、R分别为A1A、AB、AD的中点,求证:平面PQR∥平面CB1D1.