题目内容
数列{an}各项均为正数,首项为a,对任意正整数n,an•an+1=
恒成立.
(Ⅰ)若数列{an}为等比数列,求实数a的值;
(Ⅱ)记bn为数列{an}的前2n项的和,若对任意正整数n,不等式bn≤
(4n-1)恒成立,求实数a的取值范围.
| 4n |
| 2 |
(Ⅰ)若数列{an}为等比数列,求实数a的值;
(Ⅱ)记bn为数列{an}的前2n项的和,若对任意正整数n,不等式bn≤
| 11 |
| 4 |
考点:数列与不等式的综合,数列递推式
专题:等差数列与等比数列
分析:(Ⅰ)由已知条件利用递推思想依次求出a2=
,a3=4a,再由数列{an}为等比数列能求出a的值.
(Ⅱ)由已知条件知b1=a+
≤
(4-1),由此能求出实数a的取值范围.
| 2 |
| a |
(Ⅱ)由已知条件知b1=a+
| 2 |
| a |
| 11 |
| 4 |
解答:
解:(Ⅰ)∵{an}各项均为正数,首项为a,
对任意正整数n,an•an+1=
恒成立,∴a•a2=
=2,解得a2=
,
•a3=
=8,解得a3=4a,
∵数列{an}为等比数列,∴(
)2=a•4a,
解得a=1或a=-1(舍).
∴a=1.
(Ⅱ)∵bn为数列{an}的前2n项的和,
对任意正整数n,不等式bn≤
(4n-1)恒成立,
∴b1=a+
≤
(4-1),
整理,得:4a2-33a+8≤0,
解得
≤a≤8,
∴实数a的取值范围是[
,8].
对任意正整数n,an•an+1=
| 4n |
| 2 |
| 4 |
| 2 |
| 2 |
| a |
| 2 |
| a |
| 42 |
| 2 |
∵数列{an}为等比数列,∴(
| 2 |
| a |
解得a=1或a=-1(舍).
∴a=1.
(Ⅱ)∵bn为数列{an}的前2n项的和,
对任意正整数n,不等式bn≤
| 11 |
| 4 |
∴b1=a+
| 2 |
| a |
| 11 |
| 4 |
整理,得:4a2-33a+8≤0,
解得
| 1 |
| 4 |
∴实数a的取值范围是[
| 1 |
| 4 |
点评:本题考查满足等比数列的实数值的求法,考查满足不等式的实数的取值范围的求法,解题时要认真审题,注意递推思想的合理运用.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
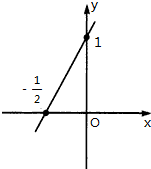 已知二次函数f(x)=ax2+bx+c(c>0且为常数)的导函数的图象如图.
已知二次函数f(x)=ax2+bx+c(c>0且为常数)的导函数的图象如图.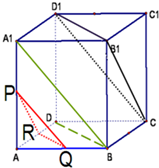 如图所示,已知正方体ABCD-A1B1C1D1中,P、Q、R分别为A1A、AB、AD的中点,求证:平面PQR∥平面CB1D1.
如图所示,已知正方体ABCD-A1B1C1D1中,P、Q、R分别为A1A、AB、AD的中点,求证:平面PQR∥平面CB1D1.