题目内容
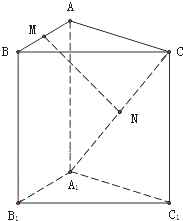在三棱柱ABC-A1B1C1中，M、N分别是AB、A1C的中点，求证：MN∥平面BCB1C1．考点：直线与平面平行的判定
专题：空间位置关系与距离
分析：连接AC1，可知N为AC1与A1C的交点，先证明出MN∥BC1，进而根据线面平行的判定定理证明出MN∥平面BCB1C1．
解答：
证明：∵四边形ACA1C1为平行四边形，
∴连接AC1，则N为AC1与A1C的交点，
∵M、N分别是AB、A1C的中点，
∴MN∥BC1，
∵BC1?平面BCB1C1，MN?平面BCB1C1，
∴MN∥平面BCB1C1．
∴连接AC1，则N为AC1与A1C的交点，
∵M、N分别是AB、A1C的中点，
∴MN∥BC1，
∵BC1?平面BCB1C1，MN?平面BCB1C1，
∴MN∥平面BCB1C1．
点评：本题主要考查了直线与平面平行的判定定理的应用．证明线面平行一般是先证明出线线平行．
练习册系列答案
相关题目
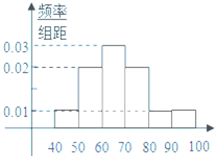某高校从参加今年自主招生考试的1000名学生中随机抽取100名学生成绩进行统计，得到如图所示的样本频率分布直方图．若规定60分及以上为合格，则估计这1000名学生中合格人数是（ ）名．| A、400 | B、600 |
| C、700 | D、800 |
过点（-1，3）且平行于直线x-2y+3=0的直线方程为（ ）
| A、x-2y=0 |
| B、2x+y-1=0 |
| C、x-2y+7=0 |
| D、2x+y-5=0 |
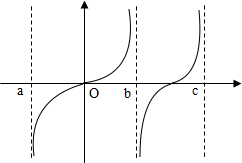已知函数f（x），x∈（a，b）∪（b，c）的图象如图所示，有三个同学对此函数的单调性作出如下的判断：
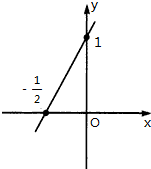已知二次函数f（x）=ax2+bx+c（c＞0且为常数）的导函数的图象如图．
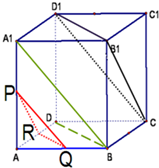如图所示，已知正方体ABCD-A1B1C1D1中，P、Q、R分别为A1A、AB、AD的中点，求证：平面PQR∥平面CB1D1．