题目内容
若有穷数列a1,a2,…an(n∈N*)满足a1=an,a2=an-1,…,an=a1,即ai=an-i+1(其中i∈N*,i≤n),就称该数列为“对称数列”.若{bn}是项数为2k-1(k∈N*)的“对称数列”,且bk,bk+1,b2k-1构成首项为50,公差为-4的等差数列,其前2k-1项和为S2k-1,则S2k-1的最大值为 .
考点:数列的函数特性,数列的求和
专题:等差数列与等比数列
分析:由于bk,bk+1,b2k-1构成首项为50,公差为-4的等差数列,可得bk=50,bk+1=46,b2k-1=44=b1,根据“对称数列”可得
S2k-1=b1+b2+b3+…+bk+bk+1+…+b2k-1=2(b1+b2+b3+…+bk)-bk再利用等差数列的前n项和公式即可得出.
S2k-1=b1+b2+b3+…+bk+bk+1+…+b2k-1=2(b1+b2+b3+…+bk)-bk再利用等差数列的前n项和公式即可得出.
解答:
解:∵bk,bk+1,b2k-1构成首项为50,公差为-4的等差数列,
∴bk=50,bk+1=46,b2k-1=44=b1,
∴S2k-1=b1+b2+b3+…+bk+bk+1+…+b2k-1
=2(b1+b2+b3+…+bk)-bk
=2[50k+
×(-4)]-50
=-4(k-13)2+626,
当k=13时,S2k-1的最大值为626.
故答案为:626.
∴bk=50,bk+1=46,b2k-1=44=b1,
∴S2k-1=b1+b2+b3+…+bk+bk+1+…+b2k-1
=2(b1+b2+b3+…+bk)-bk
=2[50k+
| k(k-1) |
| 2 |
=-4(k-13)2+626,
当k=13时,S2k-1的最大值为626.
故答案为:626.
点评:本题考查了“对称数列”、等差数列的前n项和公式、二次函数的单调性,考查了推理能力和计算能力,属于难题.

练习册系列答案
相关题目
同时掷两个骰子,则向上的点数之积是3的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
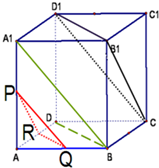 如图所示,已知正方体ABCD-A1B1C1D1中,P、Q、R分别为A1A、AB、AD的中点,求证:平面PQR∥平面CB1D1.
如图所示,已知正方体ABCD-A1B1C1D1中,P、Q、R分别为A1A、AB、AD的中点,求证:平面PQR∥平面CB1D1.