题目内容
20.已知“x>k”是“$\frac{3}{x+1}<1$”的充分不必要条件,则k的取值范围是[2,+∞).分析 解出关于$\frac{3}{x+1}<1$的x的范围,结合充分必要条件的定义,从而求出k的范围.
解答 解:由“$\frac{3}{x+1}<1$;解得:x>2或x<-1,
设集合A={x|x>k},B={x|x>2或x<-1},
“x>k”是“$\frac{3}{x+1}<1$”的充分不必要条件,
则A?B,
∴k≥2,
故答案为:[2,+∞)
点评 本题考查了充分必要条件,考查解不等式问题,是一道基础题.

练习册系列答案
相关题目
12.曲线C1的参数方程为$\left\{\begin{array}{l}x=\sqrt{10}cosθ\\ y=sinθ\end{array}$(θ为参数),圆C2:x2+(y-6)2=2,设P,Q分别为曲线C1和圆C2上的点,则P,Q两点间的最大距离是( )
| A. | 5$\sqrt{2}$ | B. | $\sqrt{46}$+$\sqrt{2}$ | C. | 7+$\sqrt{2}$ | D. | 6$\sqrt{2}$ |
9.m,n,l为不重合的直线,α,β,γ为不重合的平面,则下列说法正确的是( )
| A. | m⊥l,n⊥l,则m∥n | B. | α⊥γ,β⊥γ,则α⊥β | C. | m∥α,n∥α,则m∥n | D. | α∥γ,β∥γ,则α∥β |
10.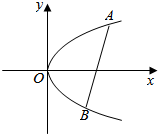 已知抛物线C的方程为y2=2px(p>0),一条长度为4p的线段AB的两个端点A、B在抛物线C上运动,则线段AB的中点D到y轴距离的最小值为 ( )
已知抛物线C的方程为y2=2px(p>0),一条长度为4p的线段AB的两个端点A、B在抛物线C上运动,则线段AB的中点D到y轴距离的最小值为 ( )
 已知抛物线C的方程为y2=2px(p>0),一条长度为4p的线段AB的两个端点A、B在抛物线C上运动,则线段AB的中点D到y轴距离的最小值为 ( )
已知抛物线C的方程为y2=2px(p>0),一条长度为4p的线段AB的两个端点A、B在抛物线C上运动,则线段AB的中点D到y轴距离的最小值为 ( )| A. | 2p | B. | $\frac{5}{2}p$ | C. | $\frac{3}{2}p$ | D. | 3p |