题目内容
10.已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;(a>b>0)$右焦点为F,又椭圆与x轴正半轴交于A点,与y轴正半轴交于点B(0,2),且$\overline{BF}•\overline{BA}=4\sqrt{2}+4$,过点D(4,0)作直线l交椭圆于不同的两点P,Q.(1)求椭圆的方程;
(2)若在x轴上的点M(m,0),使$|{\overline{MP}}|=|{\overline{MQ}}|$,求m的取值范围.
分析 (1)由题意可得B(0,b),F(c,0),D( $\frac{{a}^{2}}{c}$,0).即可表示出 $\overrightarrow{BF}$,$\overrightarrow{FD}$,$\overrightarrow{BF}$•$\overrightarrow{FD}$,又a2=b2+c2,即可得出椭圆的方程;
(2)设l的方程为y=k(x-4),与椭圆方程联立,利用△>0即可得出k的取值范围;设交点P(x1,y1),Q(x2,y2),PQ的中点R(x0,y0),利用(2)中的根与系数的关系和中点坐标公式可用k表示点R的坐标,当k=0时,容易得出M;k≠0时,若|$\overrightarrow{MP}$|=|$\overrightarrow{MQ}$|?MR⊥l?k•kMR=-1,再根据k的取值范围即可得出.
解答 解:(1)由题意可得B(0,b),F(c,0),D($\frac{{a}^{2}}{c}$,0).
于是$\overrightarrow{BF}$=(c,-b),$\overrightarrow{FD}$=($\frac{{a}^{2}}{c}$-c,0)=($\frac{{b}^{2}}{c}$,0)=(2,0).
故$\frac{{b}^{2}}{c}$=2,$\overrightarrow{BF}$•$\overrightarrow{FD}$=b2=4
∴c=2,于是a2=b2+c2=8
∴椭圆方程为$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}=1$.
(2)点D(4,0)在椭圆的外部,当直线l的斜率不存在时,直线l与椭圆C无交点,所以l的斜率存在.
故设l的方程为y=k(x-4),由$\left\{\begin{array}{l}\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}=1\\ y=k(x-4)\end{array}\right.$得(2k2+1)x2-16k2x+32k2-8=0,
依题意△=-(64k2-32)>0,k2<$\frac{1}{2}$
∴l的斜率的取值范围为-$\frac{\sqrt{2}}{2}$<k<$\frac{\sqrt{2}}{2}$.
设交点P(x1,y1),Q(x2,y2),PQ的中点R(x0,y0),则x1+x2=$\frac{16{k}^{2}}{2{k}^{2}+1}$,
x0=$\frac{{x}_{1}+{x}_{2}}{2}$=$\frac{8{k}^{2}}{2{k}^{2}+1}$,y0=k(x0-4)=k($\frac{8{k}^{2}}{2{k}^{2}+1}$-4)=$\frac{-4k}{2{k}^{2}+1}$.
当k=0时,P、Q为长轴的两个顶点.
此时M(0,0)满足|$\overrightarrow{MP}$|=|$\overrightarrow{MQ}$|,
k≠0时,若|$\overrightarrow{MP}$|=|$\overrightarrow{MQ}$|?MR⊥l?k•kMR=-1
又kMR=$\frac{4k}{2{k}^{2}+1}$÷(m-$\frac{8{k}^{2}}{2{k}^{2}+1}$)=$\frac{4k}{(2m-8){k}^{2}+m}$
由kMR•k=-1,即4k2=-(2m-8)k2-m=(8-2m)k2-m(4-2m)k2=m.
∵0<k2<$\frac{1}{2}$,∴m≠2时,k2=$\frac{m}{4-2m}$.
∴0<$\frac{m}{4-2m}$<$\frac{1}{2}$.
由$\left\{\begin{array}{l}\frac{m}{4-2m}>0\\ \frac{m}{4-2m}<\frac{1}{2}\end{array}\right.$解得$\left\{\begin{array}{l}0<m<2\\ m>2或m<1\end{array}\right.$,
∴0<m<1综上得0≤m<1.
点评 熟练掌握椭圆的标准方程及其性质、直线与椭圆的位置关系转化为方程联立得到△>0即根与系数的关系、中点坐标公式、相互垂直的直线之间的关系等是解题的关键.

 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案 如图所示,在正方形纸片ABCD中,AC与BD相交于点O,剪去△AOB,将剩余部分沿OC、OD折叠,使OA、OB重合,则在以A(B)、C、D、O为顶点的四面体中,二面角O-AD-C的余弦值为( )
如图所示,在正方形纸片ABCD中,AC与BD相交于点O,剪去△AOB,将剩余部分沿OC、OD折叠,使OA、OB重合,则在以A(B)、C、D、O为顶点的四面体中,二面角O-AD-C的余弦值为( )| A. | $\frac{\sqrt{6}}{5}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{5}}{3}$ | D. | $\frac{\sqrt{6}}{3}$ |
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{6}}{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{6}$ |
| A. | P≥Q | B. | P<Q | C. | P≤Q | D. | P>Q |
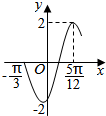
| A. | 函数f(x)的最小正周期是2π | |
| B. | 函数f(x)的图象可由函数g(x)=2sin2x的图象向右平移$\frac{π}{3}$个单位长度得到 | |
| C. | 函数f(x)的图象关于直线x=一$\frac{π}{12}$对称 | |
| D. | 函数f(x)在区间[-$\frac{7π}{12}$+kπ,-$\frac{π}{12}$+kπ](k∈Z)上是增函数 |
| A. | $\frac{5}{4}{a^2}$π | B. | a2π | C. | $\frac{3}{4}{a^2}$π | D. | $\frac{1}{4}{a^2}$π |