题目内容
函数y=
的图象大致是( )
| sin6x |
| 2x-2-x |
A、 |
B、 |
C、 |
D、 |
考点:函数的图象
专题:函数的性质及应用
分析:因为分子分母分别为奇函数,所以原函数为偶函数,排除C、D,而当x取很小的正数时,sin6x>0,2x-2-x>0,故y>0,排除B,选A
解答:
解:分别设f(x)=sin6x,g(x)=2x-2-x,
∴f(-x)=sin(-6x)=-sin6x=-f(x),g(-x)=-(2x+2-x)=-g(x),
∴函数f(x),g(x)均为奇函数,
∴所以原函数为偶函数,
故排除C,D,
而当x取很小的正数时,sin6x>0,2x-2-x>0,
故y>0,排除B,
故选:A
∴f(-x)=sin(-6x)=-sin6x=-f(x),g(-x)=-(2x+2-x)=-g(x),
∴函数f(x),g(x)均为奇函数,
∴所以原函数为偶函数,
故排除C,D,
而当x取很小的正数时,sin6x>0,2x-2-x>0,
故y>0,排除B,
故选:A
点评:本题主要考查了函数图象的识别,关键是判断出函数为偶函数,属于基础题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
已知函数y=5sinωx(ω>0)的图象与直线y-5=0相邻的两个公共点之间的距离为
,则ω的值为( )
| π |
| 2 |
A、
| ||
| B、2 | ||
C、
| ||
| D、4 |
已知抛物线y=ax2-2x+1与x轴没有交点,那么该抛物线的顶点所在的象限是( )
| A、第四象限 | B、第三象限 |
| C、第二象限 | D、第一象限 |
若函数f(x)=Asin2ωx(A>0,ω>0)在x=1处取得最大值,则f(x+1)的奇偶性为( )
| A、偶函数 |
| B、奇函数 |
| C、既是奇函数又是偶函数 |
| D、非奇非偶函数 |
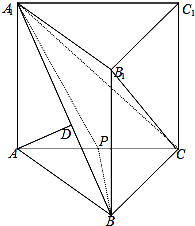 如图,直三棱柱ABC-A1B1C1中,AD⊥平面A1BC,其垂足D落在直线A1B上.P为AC的中点.
如图,直三棱柱ABC-A1B1C1中,AD⊥平面A1BC,其垂足D落在直线A1B上.P为AC的中点.