题目内容
已知正四棱锥P-ABCD的底面边长为2,侧棱长为2,则侧棱与底面所成的角的大小为 .
考点:棱锥的结构特征
专题:空间位置关系与距离
分析:如图所示,连接AC,BD,相交于点O,连接OP.根据四棱锥P-ABCD是正四棱锥,可得OP⊥底面ABCD.因此∠PAO是侧棱与底面所成的角.利用直角三角形的边角关系即可得出.
解答:
解:如图所示,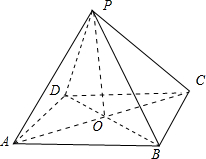
连接AC,BD,相交于点O,连接OP.
∵四棱锥P-ABCD是正四棱锥,
∴OP⊥底面ABCD.
∴∠PAO是侧棱与底面所成的角.
∵正四棱锥P-ABCD的底面边长为2,
∴AO=
AC=
.
在Rt△OAP中,cos∠PAO=
=
.
∴∠PAO=
.
故答案为:
.

连接AC,BD,相交于点O,连接OP.
∵四棱锥P-ABCD是正四棱锥,
∴OP⊥底面ABCD.
∴∠PAO是侧棱与底面所成的角.
∵正四棱锥P-ABCD的底面边长为2,
∴AO=
| 1 |
| 2 |
| 2 |
在Rt△OAP中,cos∠PAO=
| OA |
| AP |
| ||
| 2 |
∴∠PAO=
| π |
| 4 |
故答案为:
| π |
| 4 |
点评:本题考查了正四棱锥的性质、线面角、线面垂直的判定与性质、直角三角形的边角关系,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
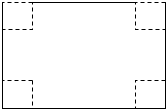 如图,一矩形铁皮的长为8cm,宽为5cm,在四个角上截去四个相同的小正方形,制成一个无盖的小盒子,问小正方形的边长为
如图,一矩形铁皮的长为8cm,宽为5cm,在四个角上截去四个相同的小正方形,制成一个无盖的小盒子,问小正方形的边长为
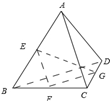 在空间四边形ABCD中,E、F、G分别在棱AB、BC、CD上,若AC∥面EFG,BD∥面EFG,
在空间四边形ABCD中,E、F、G分别在棱AB、BC、CD上,若AC∥面EFG,BD∥面EFG,