题目内容
设
,
是非零且不共线向量,若向量8
+t
与向量t2
+
共线,则实数t= .
| e1 |
| e2 |
| e1 |
| e2 |
| e1 |
| e2 |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:利用平面向量共线定理得到8
+t
与向量t2
+
的等量关系,利用向量相等求t.
| e1 |
| e2 |
| e1 |
| e2 |
解答:
解:∵向量8
+t
与向量t2
+
共线,
∴8
+t
=λ(t2
+
),整理得
,解得λ=2;
故答案为:2.
| e1 |
| e2 |
| e1 |
| e2 |
∴8
| e1 |
| e2 |
| e1 |
| e2 |
|
故答案为:2.
点评:本题考查了向量共线以及平面向量基本定理的运用;关键是利用已知向量共线得到关于t的方程组.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设a,b,c是空间三条直线,α,β是空间两个平面,则下列命题中,命题不正确的是( )
| A、当c⊥α时,若α∥β,则c⊥β |
| B、当b?α时,若α⊥β,则b⊥β |
| C、当b?α,a?α且c是a在α内的射影时,若a⊥b,则b⊥c |
| D、当b?α且c?α时,若b∥c,则c∥α |
y=|x2-2x-3|与y=k有4个不同的交点,则k的范围( )
| A、(-4,0) |
| B、[0,4] |
| C、[0,4) |
| D、(0,4) |
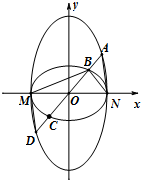 如图,曲线C1:
如图,曲线C1: 设函数f(x)=|x2-4x-5|.
设函数f(x)=|x2-4x-5|.