题目内容
下列函数中,与函数y=-e|x|的奇偶性相同,且在(-∞,0)上单调性也相同的是( )
A、y=-
| ||
| B、y=ln|x| | ||
| C、y=x3-3 | ||
| D、y=-x2+2 |
考点:奇偶性与单调性的综合
专题:函数的性质及应用
分析:根据函数奇偶性和单调性的性质即可得到结论.
解答:
解:函数y=-e|x|为偶函数,且在(-∞,0)上单调递增.
A.y=-
为奇函数,不满足条件.
B.y=ln|x|为偶函数,当x<0时,函数为y=ln(-x)单调递减.不满足条件.
C.y=x3-3为非奇非偶函数,不满足条件.
D.y=-x2+2为偶函数,在(-∞,0)上单调递增,满足条件.
故选:D
A.y=-
| 1 |
| x |
B.y=ln|x|为偶函数,当x<0时,函数为y=ln(-x)单调递减.不满足条件.
C.y=x3-3为非奇非偶函数,不满足条件.
D.y=-x2+2为偶函数,在(-∞,0)上单调递增,满足条件.
故选:D
点评:本题主要考查函数的奇偶性和单调性的应用,要求熟练掌握常见函数的奇偶性和单调性的性质.

练习册系列答案
相关题目
已知f(x)=kx+b(k<0),且f[f(x)]=4x+1,则f(x)=( )
| A、-2x-1 | ||
| B、-2x+1 | ||
| C、-x+1 | ||
D、-2x-
|
如图给出的是计算
+
+
+…+
的值的程序框图,其中判断框内应填入的是( )
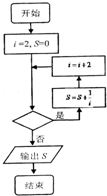
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 2014 |

| A、i≤2013 |
| B、i≤2015 |
| C、i≤2017 |
| D、i≤2019 |
已知i是虚数单位,若复数Z=a+bi(a,b∈R)在复平面内对应的点位于第四象限,则复数Z•i在复平面内对应的点位于( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
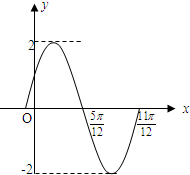 已知函数f(x)=A(sinωx+φ)(A>0,ω>0,|φ|<π)在一个周期内的图象如图所示.
已知函数f(x)=A(sinωx+φ)(A>0,ω>0,|φ|<π)在一个周期内的图象如图所示.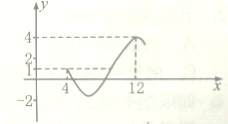 如图为函数f(x)=Asin(ωx+φ)+C(A>0,ω>0,0<φ<π)图象的一部分.
如图为函数f(x)=Asin(ωx+φ)+C(A>0,ω>0,0<φ<π)图象的一部分.