Question

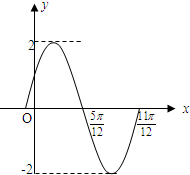已知函数f（x）=A（sinωx+φ）（A＞0，ω＞0，|φ|＜π）在一个周期内的图象如图所示．
（1）求函数的解析式；
（2）求函数的单调递增区间；
（3）当x∈[0， 

π

2

]时，求f（x）的取值范围．

Answer 1

考点：由y=Asin（ωx+φ）的部分图象确定其解析式,正弦函数的图象

专题：三角函数的求值,三角函数的图像与性质

分析：（1）根据函数的图象确定A，ω，φ的值，从而求出函数的解析式．
（2）利用整体思想求出函数的单调区间．
（3）根据函数的图象，利用函数的定义域求函数的值域．

解答： 解：（1）由图象知A=2，
T=2×(

11π

12

-

5π

12

)=π，
∴

2π

ω

=π，\
∴ω=2
由图象过点(

5π

12

，0)，
得到：2sin(

5π

6

+φ)=0，
观察图象取

5π

6

+φ=π，
得φ=

π

6

∴f(x)=2sin(2x+

π

6

)
（2）利用整体思想：
令：-

π

2

+2kπ≤2x+

π

6

≤

π

2

+2kπ，k∈Z
解得-

π

3

+kπ≤x≤

π

6

+kπ，k∈Z
故函数的单调递增区间为[-

π

3

+kπ，

π

6

+kπ]，k∈Z
（3）0≤x≤

π

2

，\
∴

π

6

≤2x+

π

6

≤

5π

6

∴f（x）的取值范围为[-1，2]．

点评：本题考查的知识要点：利用正弦型函数的图象求解析式，正弦型函数单调区间的确定，利用定义域求函数的值域．属于基础题型．