题目内容
a≤
在x∈（2，+∞）上恒成立，求a的取值范围．
| x2-x+2 |
| x-2 |
考点：函数恒成立问题
专题：不等式的解法及应用
分析：利用分离常数法求
的最小值为7，所以不等式a≤
在x∈（2，+∞）上恒成立等价于a≤7．
| x2-x+2 |
| x-2 |
| x2-x+2 |
| x-2 |
解答：
解：∵x∈（2，+∞），
∴x-2＞0．
∴
=
=（x-2）+
+3
≥4+3=7．
当且仅当x-2=2，即x=4时，“=”成立．
∵a≤
在x∈（2，+∞）上恒成立，
∴a≤7．
即a的取值范围为（-∞，7]．
∴x-2＞0．
∴
| x2-x+2 |
| x-2 |
| (x-2)2+3(x-2)+4 |
| x-2 |
=（x-2）+
| 4 |
| x-2 |
≥4+3=7．
当且仅当x-2=2，即x=4时，“=”成立．
∵a≤
| x2-x+2 |
| x-2 |
∴a≤7．
即a的取值范围为（-∞，7]．
点评：本题考查基本不等式的灵活应用，属于中档题．
练习册系列答案
举一反三同步巧讲精练系列答案
口算与应用题卡系列答案
相关题目
已知三角形ABC的三个内角A﹑B﹑C对边分别为a﹑b﹑c，则下列数值中，一定能构成三角形的三边的是（ ）
| A、a2﹑b2﹑c2 | ||||||||
B、
| ||||||||
C、1+
| ||||||||
| D、sinA﹑sinB﹑sinC |
已知L1：x-3y+7=0，L2：x+2y+4=0，下列说法正确的是（ ）
A、L1到L2的角为
| ||
B、L1到L2的角为
| ||
C、L2到L1的角为
| ||
D、L1到L2的夹角为
|
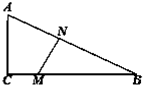有一块实验题，形如图的直角△ABC，其中∠C=90°，AC=50米，BC=120米，拟在边BC和BA之间开出一条水渠，即图示中线段MN，并且使这条水渠恰好能平分该实验题的面积．为节省人力、物力，要使这条水渠最短．问：应如何设计？水渠最短的长度为多少米？