题目内容
已知L1：x-3y+7=0，L2：x+2y+4=0，下列说法正确的是（ ）
A、L1到L2的角为
| ||
B、L1到L2的角为
| ||
C、L2到L1的角为
| ||
D、L1到L2的夹角为
|
考点：两直线的夹角与到角问题
专题：直线与圆
分析：两条直线的斜率分别为k1=
，k2=-
，设L1到L2的角为θ，则由tanθ=
的值，可得θ的值．
| 1 |
| 3 |
| 1 |
| 2 |
| k2-k1 |
| 1+k2•k1 |
解答：
解：由于L1：x-3y+7=0，L2：x+2y+4=0的斜率分别为k1=
，k2=-
，
设L1到L2的角为θ，则tanθ=
=
=-1．
结合θ∈（0，π），可得 θ=
，
故选：A．
| 1 |
| 3 |
| 1 |
| 2 |
设L1到L2的角为θ，则tanθ=
| k2-k1 |
| 1+k2•k1 |
-
| ||||
1-
|
结合θ∈（0，π），可得 θ=
| 3π |
| 4 |
故选：A．
点评：本题主要考查一条直线到另一条直线的夹角公式的应用，属于中档题．
练习册系列答案
相关题目
曲线y=2x4上的点到直线y=-x-1的距离的最小值为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知A={2，a}，B={1，2，3}，则“a=3”是“A⊆B”的（ ）
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充要条件 |
| D、既非充分亦非必要条件 |
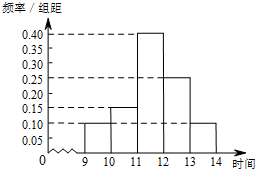某商场在国庆黄金周的促销活动中，对10月1日9时至14时的销售额进行统计，其频率分布直方图如图所示．已知9时至10时的销售额为3万元，则11时至12时的销售额为（ ）| A、8万元 | B、10万元 |
| C、12万元 | D、15万 |
在复平面内，设z=1+i（i是虚数单位），则复数
+z2对应的点位于（ ）
| 2 |
| z |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
一个几何体的三视图如图所示，则这个几何体的表面积为（ ）
A、7+
| ||
B、9+
| ||
C、7+
| ||
D、9+
|