题目内容
已知函数f(x)=
,其a中为常数,a≤2.
(Ⅰ)当a=1时,求曲线y=f(x)在点(0,f(0))处的切线方程;
(Ⅱ)是否存在实数a,使f(x)的极大值为2?若存在,求出a的值;若不存在,说明理由.
| x2+ax+a |
| ex |
(Ⅰ)当a=1时,求曲线y=f(x)在点(0,f(0))处的切线方程;
(Ⅱ)是否存在实数a,使f(x)的极大值为2?若存在,求出a的值;若不存在,说明理由.
考点:利用导数研究函数的极值,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(Ⅰ)把a=1代入函数解析式,求出f(0),求出原函数的导函数,得到f′(0),则由直线方程的点斜式得到曲线y=f(x)在点(0,f(0))处的切线方程;
(Ⅱ)对原函数求导,由导函数等于0得到导函数的零点,当a=2时,导函数恒小于等于0,原函数在定义域内递减,函数无极值;当a<2时,由函数零点的定义域分段,判断导函数在不同区间段内的符号,得到原函数的单调性,得到函数的极大值,再由导数求得极大值的范围,则问题得到判断.
(Ⅱ)对原函数求导,由导函数等于0得到导函数的零点,当a=2时,导函数恒小于等于0,原函数在定义域内递减,函数无极值;当a<2时,由函数零点的定义域分段,判断导函数在不同区间段内的符号,得到原函数的单调性,得到函数的极大值,再由导数求得极大值的范围,则问题得到判断.
解答:
解:(Ⅰ)当a=1时,f(x)=
,f(0)=
=1.
∵f′(x)=
=
=
,
∴f′(0)=0.
则曲线在点(0,f(0))处的切线方程为y=1;
(Ⅱ)由f(x)=
,得
f′(x)=
=
.
由f′(x)=0,得x1=0,x2=2-a,
∵a≤2,
∴2-a≥0.
当a=2时,f′(x)=
≤0,
∴f(x)在(-∞,+∞)上递减,无极值;
当a<2时,2-a>0,f(x)在(-∞,2),(2-a,+∞)上递减,在(0,2-a)上递增;
∴f(2-a)=(4-a)ea-2为f(x)的极大值,
令u(a)=(4-a)ea-2(a<2),则u′(a)=(3-a)ea-2>0,
∴u(a)在(-∞,2)上递增,
∴u(a)<u(2)=2,
∴不存在实数a,使f(x)的极大值为2.
| x2+x+1 |
| ex |
| 1 |
| e0 |
∵f′(x)=
| (2x+1)ex-ex(x2+x+1) |
| e2x |
| -x2+x |
| ex |
| -x(x-1) |
| ex |
∴f′(0)=0.
则曲线在点(0,f(0))处的切线方程为y=1;
(Ⅱ)由f(x)=
| x2+ax+a |
| ex |
f′(x)=
| (2x+a)ex-ex(x2+ax+a) |
| e2x |
| -x[x-(2-a)] |
| ex |
由f′(x)=0,得x1=0,x2=2-a,
∵a≤2,
∴2-a≥0.
当a=2时,f′(x)=
| -x2 |
| ex |
∴f(x)在(-∞,+∞)上递减,无极值;
当a<2时,2-a>0,f(x)在(-∞,2),(2-a,+∞)上递减,在(0,2-a)上递增;
∴f(2-a)=(4-a)ea-2为f(x)的极大值,
令u(a)=(4-a)ea-2(a<2),则u′(a)=(3-a)ea-2>0,
∴u(a)在(-∞,2)上递增,
∴u(a)<u(2)=2,
∴不存在实数a,使f(x)的极大值为2.
点评:本题考查利用导数研究曲线上某点处的切线方程,考查了利用导数求函数的极值,解答此题(Ⅱ)的关键是求解函数极值的范围,是中高档题.

练习册系列答案
相关题目
在△ABC中,角A,B,C所对的边分别为a,b,c,若A=120°,B=45°,a=
,则b=( )
| 2 |
| A、2 | ||||
B、
| ||||
C、
| ||||
D、
|
在复平面内,设z=1+i(i是虚数单位),则复数
+z2对应的点位于( )
| 2 |
| z |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
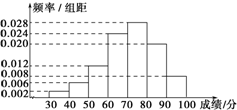 某中学为了解学生数学课程的学习情况,在3000名学生中随机抽取200名,并统计这200名学生的某次数学考试成绩,得到了样本的频率分布直方图(如图).根据频率分布直方图推测,这3000名学生在该次数学考试中成绩小于60分的学生数是
某中学为了解学生数学课程的学习情况,在3000名学生中随机抽取200名,并统计这200名学生的某次数学考试成绩,得到了样本的频率分布直方图(如图).根据频率分布直方图推测,这3000名学生在该次数学考试中成绩小于60分的学生数是