题目内容
不等式sin2θ-(2
+
a)sin(θ+
)-
>-3-2a对θ∈[0,
]恒成立.对于上面的不等式小川同学设x=sinθ+cosθ,则有sin2θ=x2-1,请照这一思路将不等式左边化为关于x的函数y=h(x)
(1)求函数y=h(x)的解析式与定义域
(2)求实数a的取值范围.
| 2 |
| 2 |
| π |
| 4 |
2
| ||
cos(θ-
|
| π |
| 2 |
(1)求函数y=h(x)的解析式与定义域
(2)求实数a的取值范围.
考点:函数解析式的求解及常用方法
专题:函数的性质及应用
分析:(1)首先,根据x=sinθ+cosθ,得到x=
sin(x+
),然后,确定函数的定义域,再利用sin(x+
)=sin(x-
)代人化简,得到函数y=h(x)的解析式.
(2)分离参数a然后,借助于基本不等式进行求解范围问题.
| 2 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
(2)分离参数a然后,借助于基本不等式进行求解范围问题.
解答:
解:(1)∵x=sinθ+cosθ,
∴x=
sin(θ+
),
∵θ∈[0,
],
∴θ+
∈[
,
],
∴x∈[1,
],
函数的定义域为[1,
];
∵sin2θ=x2-1,x=
sin(θ+
),
sin(θ+
)=cos(θ-
)=
x,
∴函数y=h(x)=x2-1-(2
+
a)
x-
=x2-(a+2)x-
-1,
∴y=h(x)=x2-(a+2)x-
-1,
(2)∵h(x)=x2-(a+2)x-
-1>-3-2a,
即x2-(a+2)x-
-1+3+2a>0,
∴(2-x)a>2x-x2+
=x(x-2)+2×
,
∵x∈[1,
],
∴2-x>0,
∴a>x+
,
令函数f(x)=x+
,
则函数f(x)在x∈[1,
] 上单调递减,
所以f(x)在x∈[1,
] 上的最大值为f(1)=3.
即知a的取值范围为(3,+∞).
∴x=
| 2 |
| π |
| 4 |
∵θ∈[0,
| π |
| 2 |
∴θ+
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
∴x∈[1,
| 2 |
函数的定义域为[1,
| 2 |
∵sin2θ=x2-1,x=
| 2 |
| π |
| 4 |
sin(θ+
| π |
| 4 |
| π |
| 4 |
| ||
| 2 |
∴函数y=h(x)=x2-1-(2
| 2 |
| 2 |
| ||
| 2 |
2
| ||||
|
=x2-(a+2)x-
| 4 |
| x |
∴y=h(x)=x2-(a+2)x-
| 4 |
| x |
(2)∵h(x)=x2-(a+2)x-
| 4 |
| x |
即x2-(a+2)x-
| 4 |
| x |
∴(2-x)a>2x-x2+
| 4-2x |
| x |
| 2-x |
| x |
∵x∈[1,
| 2 |
∴2-x>0,
∴a>x+
| 2 |
| x |
令函数f(x)=x+
| 2 |
| x |
则函数f(x)在x∈[1,
| 2 |
所以f(x)在x∈[1,
| 2 |
即知a的取值范围为(3,+∞).
点评:本题综合考查函数的基本性质,函数恒成立问题,分离参数法在求解问题中的灵活运用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
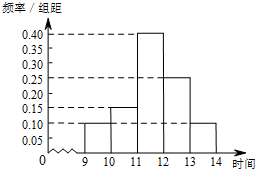 某商场在国庆黄金周的促销活动中,对10月1日9时至14时的销售额进行统计,其频率分布直方图如图所示.已知9时至10时的销售额为3万元,则11时至12时的销售额为( )
某商场在国庆黄金周的促销活动中,对10月1日9时至14时的销售额进行统计,其频率分布直方图如图所示.已知9时至10时的销售额为3万元,则11时至12时的销售额为( )| A、8万元 | B、10万元 |
| C、12万元 | D、15万 |
 如图:在直三棱柱ABC-A1B1C1中,AC=BC=C1C,AC⊥CB,D为AB的中点,
如图:在直三棱柱ABC-A1B1C1中,AC=BC=C1C,AC⊥CB,D为AB的中点,