题目内容
已知函数f(x)是定义域为(-∞,1]的增函数,
(1)若f(x-2)<f(-
),求x的取值范围;
(2)是否存在实数a,使得f(a-sinx)≤f(a2-sin2x)对一切x∈R恒成立?若不存在,请说明理由;若存在,求出a的值.
(1)若f(x-2)<f(-
| 1 |
| x |
(2)是否存在实数a,使得f(a-sinx)≤f(a2-sin2x)对一切x∈R恒成立?若不存在,请说明理由;若存在,求出a的值.
考点:函数恒成立问题,函数单调性的性质
专题:综合题,函数的性质及应用
分析:(1)利用函数的单调性,结合函数的定义域,转化为具体不等式,即可求x的取值范围;
(2)假设存在实数a,使得f(a-sinx)≤f(a2-sin2x)对一切x∈R恒成立,只需
,由此结合三角函数的最值加以计算,即可确定存在实数a的值.
(2)假设存在实数a,使得f(a-sinx)≤f(a2-sin2x)对一切x∈R恒成立,只需
|
解答:
解:(1)∵函数f(x)是定义域为(-∞,1]的增函数,f(x-2)<f(-
),
∴
,∴x≤-1-------(5分)
(2)假设存在实数a,使得f(a-sinx)≤f(a2-sin2x)对一切x∈R恒成立,
则
即
--(8分)
只需
,-------(10分)
又sin2x-sinx=(sinx-
)2-
且-1≤sinx≤1,∴(sin2x-sinx)max=2
又(1+sin2x)min=1,
∴
-------(13分)
解得a=-1,
∴存在实数a=-1,使得f(a-sinx)≤f(a2-sin2x)对一切x∈R恒成立.-----(14分)
| 1 |
| x |
∴
|
(2)假设存在实数a,使得f(a-sinx)≤f(a2-sin2x)对一切x∈R恒成立,
则
|
|
只需
|
又sin2x-sinx=(sinx-
| 1 |
| 2 |
| 1 |
| 4 |
又(1+sin2x)min=1,
∴
|
解得a=-1,
∴存在实数a=-1,使得f(a-sinx)≤f(a2-sin2x)对一切x∈R恒成立.-----(14分)
点评:本题探索不等式恒成立的k值是否存在,着重考查了函数的单调性、三角函数的最值的函数恒成立问题的讨论等知识,属于中档题.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
若x,y均为区间(0,1)的随机数,则2x-y>0的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
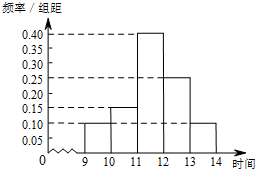 某商场在国庆黄金周的促销活动中,对10月1日9时至14时的销售额进行统计,其频率分布直方图如图所示.已知9时至10时的销售额为3万元,则11时至12时的销售额为( )
某商场在国庆黄金周的促销活动中,对10月1日9时至14时的销售额进行统计,其频率分布直方图如图所示.已知9时至10时的销售额为3万元,则11时至12时的销售额为( )| A、8万元 | B、10万元 |
| C、12万元 | D、15万 |
一个几何体的三视图如图所示,则这个几何体的表面积为( )


A、7+
| ||
B、9+
| ||
C、7+
| ||
D、9+
|