题目内容
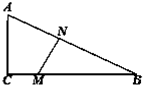有一块实验题，形如图的直角△ABC，其中∠C=90°，AC=50米，BC=120米，拟在边BC和BA之间开出一条水渠，即图示中线段MN，并且使这条水渠恰好能平分该实验题的面积．为节省人力、物力，要使这条水渠最短．问：应如何设计？水渠最短的长度为多少米？考点：解三角形的实际应用
专题：应用题,解三角形
分析：利用
=
=
，求出BM•BN，在△MBN中，利用余弦定理，结合基本不等式，即可求出结论．
| S△BMN |
| S△BCA |
| BM•BN |
| BC•BA |
| 1 |
| 2 |
解答：
解：首先
=
=
⇒BM•BN=
•120•130=7800…（2分）
在△MBN中，注意到cosB=
，
由余弦定理得MN=
=
≥
=20
…（8分）
取等条件是BM=BN=10
，
答：当BM=BN=10
米时，水渠长度的最小值为20
米．…（12分）
| S△BMN |
| S△BCA |
| BM•BN |
| BC•BA |
| 1 |
| 2 |
| 1 |
| 2 |
在△MBN中，注意到cosB=
| 12 |
| 13 |
由余弦定理得MN=
| BM2+BN2-2BM•BN•cosB |
| BM2+BN2-14400 |
| 2BM•BN-14400 |
| 3 |
取等条件是BM=BN=10
| 78 |
答：当BM=BN=10
| 78 |
| 3 |
点评：本题考查解三角形的实际应用，考查余弦定理、基本不等式的运用，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
在下列命题中，正确命题的个数是（ ）
①两个复数不能比较大小；
②复数z=i-1对应的点在第四象限；
③若（x2-1）+（x2+3x+2）i是纯虚数，则实数x=±1；
④若（z1-z2）2+（z2-z3）2=0，则z1=z2=z3．
①两个复数不能比较大小；
②复数z=i-1对应的点在第四象限；
③若（x2-1）+（x2+3x+2）i是纯虚数，则实数x=±1；
④若（z1-z2）2+（z2-z3）2=0，则z1=z2=z3．
| A、0 | B、1 | C、2 | D、3 |
一个几何体的三视图如图所示，则这个几何体的表面积为（ ）
A、7+
| ||
B、9+
| ||
C、7+
| ||
D、9+
|
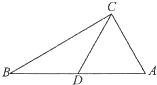如图在△ABC中，已知∠A=
如图：在直三棱柱ABC-A1B1C1中，AC=BC=C1C，AC⊥CB，D为AB的中点，