Question

设点F₁（-c，0），F₂（c，0）分别是椭圆C：

x2

a2

+y2=1（a＞1）的左、右焦点，P为椭圆C上任意一点，且

PF1

•

PF2

的最小值为0．
（1）求椭圆C的方程；
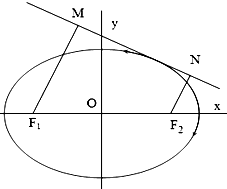
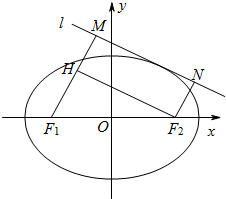
（2）如图，动直线l：y=kx+m与椭圆C有且仅有一个公共点，点M，N是直线l上的两点，且F₁M⊥l，F₂N⊥l，求四边形F₁MNF₂面积S的最大值．

Answer 1

考点：直线与圆锥曲线的综合问题

专题：综合题,圆锥曲线的定义、性质与方程

分析：（1）利用

PF1

•

PF2

的最小值为0，可得

PF1

•

PF2

=x²+y²-c²=

a2-1

a2

x²+1-c²，x∈[-a，a]，即可求椭圆C的方程；
（2）将直线l的方程y=kx+m代入椭圆C的方程中，得到关于x的一元二次方程，由直线l与椭圆C仅有一个公共点知，△=0，即可得到m，k的关系式，利用点到直线的距离公式即可得到d₁=|F₁M|，d₂=|F₂N|．当k≠0时，设直线l的倾斜角为θ，则|d₁-d₂|=|MN|×|tanθ|，即可得到四边形F₁MNF₂面积S的表达式，利用基本不等式的性质，结合当k=0时，四边形F₁MNF₂是矩形，即可得出S的最大值．

解答： 解：（1）设P（x，y），则

F1P

=（x+c，y），

F2P

=（x-c，y），
∴

PF1

•

PF2

=x²+y²-c²=

a2-1

a2

x²+1-c²，x∈[-a，a]，
由题意得，1-c²=0⇒c=1⇒a²=2，
∴椭圆C的方程为

x2

2

+y2=1；  
（2）将直线l的方程y=kx+m代入椭圆C的方程x²+2y²=2中，得（2k²+1）x²+4kmx+2m²-2=0．                
由直线l与椭圆C仅有一个公共点知，△=16k²m²-4（2k²+1）（2m²-2）=0，
化简得：m²=2k²+1．                          
设d₁=|F₁M|=

|-k+m|

k2+1

，d₂=|F₂N|=

|k+m|

k2+1

，
当k≠0时，设直线l的倾斜角为θ，
则|d₁-d₂|=|MN|×|tanθ|，
∴|MN|=

1

|k|

•|d₁-d₂|，
∴S=

1

2

•

1

|k|

•d₁-d₂|•（d₁+d₂）=

2|m|

k2+1

=

4|m|

m2+1

=

4

|m|+ 1 |m|

，
∵m²=2k²+1，∴当k≠0时，|m|＞1，|m|+

1

|m|

＞2，
∴S＜2．
当k=0时，四边形F₁MNF₂是矩形，S=2．   
所以四边形F₁MNF₂面积S的最大值为2．

点评：本题主要考查椭圆的方程与性质、直线方程、直线与椭圆的位置关系、向量知识、二次函数的单调性、基本不等式的性质等基础知识，考查运算能力、推理论证以及分析问题、解决问题的能力，考查数形结合、化归与转化思想．