题目内容
9.在新年联欢晚会上,游戏获胜者甲和乙各有一次抽奖机会,共有4个奖品,其中一等奖2个,二等奖2个,甲、乙二人依次各抽一次.(Ⅰ)求甲抽到一等奖,乙抽到二等奖的概率;
(Ⅱ)求甲、乙二人中至少有一人抽到一等奖的概率.
分析 (Ⅰ)利用相互独立事件概率乘法公式能求出甲抽到一等奖,乙抽到二等奖的概率.
(Ⅱ)甲、乙二人中至少有一人抽到一等奖的对立事件是甲、乙二人都抽到二等奖,由此利用对立事件概率计算公式能求出甲、乙二人中至少有一人抽到一等奖的概率.
解答 (本题满分10分)
解:(Ⅰ)∵游戏获胜者甲和乙各有一次抽奖机会,共有4个奖品,
其中一等奖2个,二等奖2个,甲、乙二人依次各抽一次.
∴甲抽到一等奖,乙抽到二等奖的概率:
p1=$\frac{2}{4}×\frac{2}{3}$=$\frac{1}{3}$.
(Ⅱ)甲、乙二人中至少有一人抽到一等奖的对立事件是甲、乙二人都抽到二等奖,
∴甲、乙二人中至少有一人抽到一等奖的概率:
p2=1-$\frac{2}{4}×\frac{1}{3}$=$\frac{5}{6}$.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意相互独立事件概率乘法公式、对立事件概率计算公式的合理运用.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
17.函数f(x)=x+$\frac{1}{2x}$,x∈($\frac{1}{2}$,2),若f(x)-m>0对一切x∈($\frac{1}{2}$,2)恒成立,则实数m的取值范围为( )
| A. | (-∞,$\frac{\sqrt{2}}{2}$) | B. | (-∞,$\sqrt{2}$) | C. | (-∞,$\frac{3}{2}$) | D. | ($\frac{3}{2}$,$\frac{9}{4}$) |
14.某电影公司2012年大陆电影票房为21亿元,若该公司大陆电影票房的年平均增长率为x,2016年大陆电影票房为y亿元,则y与x的函数关系式为( )
| A. | y=84x | B. | y=21(1+4x) | C. | y=21x4 | D. | y=21(1+x)4 |
18.设集合M={x|x2=x},N={x|1<2x<2},则M∪N=( )
| A. | (-∞,2] | B. | (0,1] | C. | (0,2] | D. | [0,1] |
19.某校高三文科600名学生参加了12月的模拟考试,学校为了了解高三文科学生的数学、外语情况,利用随机数表法从中抽取100名学生的成绩进行统计分析,抽出的100名学生的数学、外语成绩如表:
(Ⅰ)若数学成绩优秀率为35%,求m,n的值;
(Ⅱ)在外语成绩为良的学生中,已知m≥12,n≥10,求数学成绩优比良的人数少的概率.
| 外语 | ||||
| 优 | 良 | 及格 | ||
| 数学 | 优 | 8 | m | 9 |
| 良 | 9 | n | 11 | |
| 及格 | 8 | 9 | 11 | |
(Ⅱ)在外语成绩为良的学生中,已知m≥12,n≥10,求数学成绩优比良的人数少的概率.
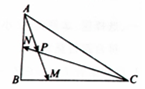 在△ABC中,$\overrightarrow{AM}$=$\frac{3}{4}$$\overrightarrow{AB}$+$\frac{1}{4}$$\overrightarrow{AC}$
在△ABC中,$\overrightarrow{AM}$=$\frac{3}{4}$$\overrightarrow{AB}$+$\frac{1}{4}$$\overrightarrow{AC}$