题目内容
17.函数f(x)=x+$\frac{1}{2x}$,x∈($\frac{1}{2}$,2),若f(x)-m>0对一切x∈($\frac{1}{2}$,2)恒成立,则实数m的取值范围为( )| A. | (-∞,$\frac{\sqrt{2}}{2}$) | B. | (-∞,$\sqrt{2}$) | C. | (-∞,$\frac{3}{2}$) | D. | ($\frac{3}{2}$,$\frac{9}{4}$) |
分析 由题意知f(x)-m>0对一切x∈($\frac{1}{2}$,2)恒成立,可转化为:m<x+$\frac{1}{2x}$ 在($\frac{1}{2}$,2)上恒成立.
解答 解:∵f(x)-m>0 即 f(x)>m⇒m<x+$\frac{1}{2x}$;
令h(x)=x+$\frac{1}{2x}$
h'(x)=1-$\frac{1}{2}$•$\frac{1}{{x}^{2}}$,令h'(x)=0⇒x=±$\frac{\sqrt{2}}{2}$ (负舍);
所以,h(x)在($\frac{1}{2}$,$\frac{\sqrt{2}}{2}$)上单调递减,($\frac{\sqrt{2}}{2}$,2)上单调递增;
∴h(x)min=$\sqrt{2}$;
所以,m的取值范围为(-∞,$\sqrt{2}$);
故选:B
点评 本题主要考察了对勾函数、利用导数判断原函数单调性以及函数恒成立问题,属中等题.

练习册系列答案
相关题目
20.已知a>1,f(x)=x2-ax,当x∈(-1,1)时,均有f(x)<$\frac{2}{3}$,则实数a的取值范围是( )
| A. | (1,2) | B. | (1,3] | C. | (1,$\frac{3}{2}$) | D. | (1,2] |
2.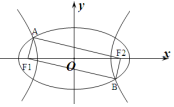 如图F1、F2是椭圆C1:$\frac{{x}^{2}}{4}$+y2=1与双曲线C2的公共焦点,A、B分别是C1、C2在第二、四象限的公共点,若四边形AF1BF2为矩形,则C2的离心率是( )
如图F1、F2是椭圆C1:$\frac{{x}^{2}}{4}$+y2=1与双曲线C2的公共焦点,A、B分别是C1、C2在第二、四象限的公共点,若四边形AF1BF2为矩形,则C2的离心率是( )
 如图F1、F2是椭圆C1:$\frac{{x}^{2}}{4}$+y2=1与双曲线C2的公共焦点,A、B分别是C1、C2在第二、四象限的公共点,若四边形AF1BF2为矩形,则C2的离心率是( )
如图F1、F2是椭圆C1:$\frac{{x}^{2}}{4}$+y2=1与双曲线C2的公共焦点,A、B分别是C1、C2在第二、四象限的公共点,若四边形AF1BF2为矩形,则C2的离心率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{6}}{2}$ |
6.已知f(x)为偶函数,且f(x)=f(x-4),在区间[0,2]上,f(x)=$\left\{\begin{array}{l}{-{x}^{2}-\frac{3}{2}x+5,0≤x≤1}\\{{2}^{x}+{2}^{-x},a<x≤2}\end{array}\right.$,g(x)=($\frac{1}{2}$)|x|+a,若F(x)=f(x)-g(x)恰好有4个零点,则a的取值范围是( )
| A. | (2,$\frac{19}{8}$) | B. | (2,3) | C. | (2,$\frac{19}{8}$] | D. | (2,3] |