题目内容
12.已知圆O:x2+y2=4,直线l:mx-y+1=0与圆O交于点A,C,直线n:x+my-m=0与圆O交于点B,D,则四边形ABCD面积的最大值是7.分析 先确定直线m,n恒过定点M(0,1),圆心O(0,0),半径R=2,AC2+BD2为定值,表示出面积,即可求四边形ABCD的面积的最大值和最小值.
解答 解:由题意可得,直线m,n恒过定点M(0,1),圆心O(0,0),半径R=2,
设弦AC,BD的中点分别为E,F,则OE2+OF2=OM2=1,
∴AC2+BD2=4(8-OE2-OF2)=28,
∴S2≤$\frac{1}{4}$AC2•BD2=$\frac{1}{4}$AC2•(28-AC2)≤$\frac{1}{4}•(\frac{A{C}^{2}+28-A{C}^{2}}{2})^{2}$=49,
∴S≤7,当且仅当AC2=28-AC2,即AC=$\sqrt{14}$时,取等号,
故四边形ABCD面积S的最大值为7.
故答案为:7.
点评 本题主要考查直线过定点,考查面积的计算,基本不等式的应用,正确运用代入法是解题的关键,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.已知a>1,f(x)=x2-ax,当x∈(-1,1)时,均有f(x)<$\frac{2}{3}$,则实数a的取值范围是( )
| A. | (1,2) | B. | (1,3] | C. | (1,$\frac{3}{2}$) | D. | (1,2] |
17.过抛物线x2=4y焦点F的直线交抛物线于A,B两点,若|AF|=3,则|BF|的值为( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | 1 | D. | $\frac{3}{2}$ |
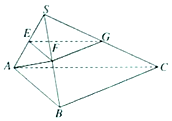 如图,在三棱锥S-ABC中,平面SAB⊥平面SBC,AB⊥BC,AS=AB,点E、F、G分别是棱SA、SB、SC的中点.求证:
如图,在三棱锥S-ABC中,平面SAB⊥平面SBC,AB⊥BC,AS=AB,点E、F、G分别是棱SA、SB、SC的中点.求证: