题目内容
4.$lg2+lg5-\root{4}{2}×{8^{0.25}}-{2017^0}$=-2.分析 根据指数幂和对数的运算性质计算即可.
解答 解:原式=lg10-${2}^{\frac{1}{4}}•{2}^{\frac{3}{4}}$-1=1-2-1=-2.
故答案为:-2
点评 本题考查了指数幂和对数的运算性质,属于基础题.

练习册系列答案
相关题目
8.$\root{3}{(lg50-1)^{3}}$-$\sqrt{(lg2-1)^{2}}$=( )
| A. | 2lg5 | B. | 0 | C. | -1 | D. | -2lg5 |
19.已知F1、F2是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点,点P是该双曲线上的任意一点,若△PF1F2的内切圆半径为r,则r的取值范围是( )
| A. | (0,a) | B. | (0,b) | C. | (0,$\sqrt{{a}^{2}+{b}^{2}}$) | D. | (0,$\sqrt{ab}$) |
16.若函数$f(x)=sin(\frac{1}{2}x+\frac{π}{6})$,则f(x)( )
| A. | 图象关于$x=\frac{π}{3}$对称 | |
| B. | 图象关于$(\frac{2π}{3},0)$对称 | |
| C. | 在$[\frac{2π}{3},\frac{8π}{3}]$上单调递减 | |
| D. | 单调递增区间是$[2kπ-\frac{4π}{3},2kπ+\frac{2π}{3}](k∈Z)$ |
13.已知i为虚数单位,则$\frac{1-i}{i^3}$=( )
| A. | 1+i | B. | 1-i | C. | -1-i | D. | -1+i |
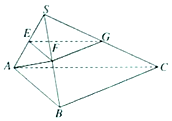 如图,在三棱锥S-ABC中,平面SAB⊥平面SBC,AB⊥BC,AS=AB,点E、F、G分别是棱SA、SB、SC的中点.求证:
如图,在三棱锥S-ABC中,平面SAB⊥平面SBC,AB⊥BC,AS=AB,点E、F、G分别是棱SA、SB、SC的中点.求证: