题目内容
14．某电影公司2012年大陆电影票房为21亿元，若该公司大陆电影票房的年平均增长率为x，2016年大陆电影票房为y亿元，则y与x的函数关系式为（ ）| A． | y=84x | B． | y=21（1+4x） | C． | y=21x4 | D． | y=21（1+x）4 |
分析 根据题意，2012年大陆电影票房为21亿元，年平均增长率为x，则2013年为21（1+x），依此类推，可得2016年大陆电影票房．
解答 解：由题意：2012年大陆电影票房为21亿元，年平均增长率为x，则2016年大陆电影票房为21（1+x）4，
即y=21（1+x）4，
∴y与x的函数关系式为y=21（1+x）4，
故选：D．
点评 本题考查了实际问题的增长率问题，属于基础题．
练习册系列答案
名题训练系列答案
期末集结号系列答案
相关题目
17．过抛物线x2=4y焦点F的直线交抛物线于A，B两点，若|AF|=3，则|BF|的值为（ ）
| A． | 2 | B． | $\frac{1}{2}$ | C． | 1 | D． | $\frac{3}{2}$ |
2．
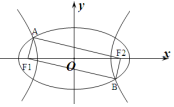如图F1、F2是椭圆C1：$\frac{{x}^{2}}{4}$+y2=1与双曲线C2的公共焦点，A、B分别是C1、C2在第二、四象限的公共点，若四边形AF1BF2为矩形，则C2的离心率是（ ）
如图F1、F2是椭圆C1：$\frac{{x}^{2}}{4}$+y2=1与双曲线C2的公共焦点，A、B分别是C1、C2在第二、四象限的公共点，若四边形AF1BF2为矩形，则C2的离心率是（ ）| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | $\frac{\sqrt{6}}{2}$ |
6．已知f（x）为偶函数，且f（x）=f（x-4），在区间[0，2]上，f（x）=$\left\{\begin{array}{l}{-{x}^{2}-\frac{3}{2}x+5，0≤x≤1}\\{{2}^{x}+{2}^{-x}，a＜x≤2}\end{array}\right.$，g（x）=（$\frac{1}{2}$）|x|+a，若F（x）=f（x）-g（x）恰好有4个零点，则a的取值范围是（ ）
| A． | （2，$\frac{19}{8}$） | B． | （2，3） | C． | （2，$\frac{19}{8}$] | D． | （2，3] |
3．已知函数f（x）=x3+x-1，则在下列区间中，f（x）一定有零点的是（ ）
| A． | （-1，0） | B． | （0，1） | C． | （-2，-1） | D． | （1，2） |
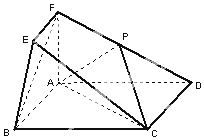在如图所示的几何体中，四边形ABCD为矩形，平面ABEF⊥平面ABCD，EF∥AB，∠BAF=90°，AD=2，AB=AF=2EF=l，点P在棱DF上．