题目内容
若向量
=(
sinωx,cosωx),b=(cosωx,cosωx),ω>0,x∈R,f(x)=a•b-
,且f(x)的周期是π,设△ABC三个角A,B,C的对边分别为a,b,c
(Ⅰ)求ω的值;
(Ⅱ)若c=
,f(C)=
,sinB=3sinA,求a,b的值.
| a |
| 3 |
| 1 |
| 2 |
(Ⅰ)求ω的值;
(Ⅱ)若c=
| 7 |
| 1 |
| 2 |
考点:余弦定理,平面向量数量积的运算,两角和与差的正弦函数
专题:三角函数的图像与性质,解三角形
分析:(Ⅰ)化简函数解析式可得f(x)=sin(2ωx+
),由T=
=
=π即可解得ω.
(Ⅱ)由f(C)=sin(2C+
)=
,可得C=
,由余弦定理可得a2+b2-ab=7①,由已知及正弦定理可得:b=3a②,联立即可解得a,b的值.
| π |
| 6 |
| 2π |
| 2ω |
| π |
| ω |
(Ⅱ)由f(C)=sin(2C+
| π |
| 6 |
| 1 |
| 2 |
| π |
| 3 |
解答:
解:(Ⅰ)f(x)=a•b-
=
sinωxcosωx+cos2ωx-
=
sin2ωx+
cos2ωx
=sin(2ωx+
)
由T=
=
=π
解得:ω=1
(Ⅱ)∵f(C)=sin(2C+
)=
,
∴2C+
=
(舍去)或2C+
=
,
∴C=
由余弦定理可得:7=a2+b2-2abcos
即有:a2+b2-ab=7①
∵sinB=3sinA
∴由正弦定理可得:b=3a②
由①②即可解得:a=1,b=3
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
=
| ||
| 2 |
| 1 |
| 2 |
=sin(2ωx+
| π |
| 6 |
由T=
| 2π |
| 2ω |
| π |
| ω |
解得:ω=1
(Ⅱ)∵f(C)=sin(2C+
| π |
| 6 |
| 1 |
| 2 |
∴2C+
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
∴C=
| π |
| 3 |
由余弦定理可得:7=a2+b2-2abcos
| π |
| 3 |
即有:a2+b2-ab=7①
∵sinB=3sinA
∴由正弦定理可得:b=3a②
由①②即可解得:a=1,b=3
点评:此题考查了正弦定理、余弦定理,平面向量数量积的运算以及特殊角的三角函数值的应用,考查了两角和与差的正弦函数公式的应用,熟练掌握公式及相关定理是解本题的关键,属于基本知识的考查.

练习册系列答案
相关题目
若(x+
)4=a0+a1x+a2x2+a3x3+a4x4,则(a0+a2+a4)2-(a1+a3)2的值为( )
| 3 |
| A、-16 | ||
| B、16 | ||
C、
| ||
D、
|
 如图,AB是半圆O的直径,BD与AC相交于点E,且OE⊥AC.若BE=3DE=3,则AC的长为
如图,AB是半圆O的直径,BD与AC相交于点E,且OE⊥AC.若BE=3DE=3,则AC的长为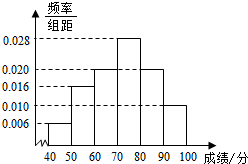 某校高三文科(1)班学生参加“江南十校”联考,其数学成绩(已折合成百分制)的频率分布直方图如图所示,其中成绩分布敬意为[40,50),[50,60),[60,70),[70,80),[80,90),[90,100],现已知成绩落在[90,100]的有5人.
某校高三文科(1)班学生参加“江南十校”联考,其数学成绩(已折合成百分制)的频率分布直方图如图所示,其中成绩分布敬意为[40,50),[50,60),[60,70),[70,80),[80,90),[90,100],现已知成绩落在[90,100]的有5人.