题目内容
把一颗骰子投掷两次,观察出现的点数,并记第一次出现的点数为a,第二次出现的点数为b,试就方程组
解答下列问题:
(I)求方程组有解的概率;
(Ⅱ)求以方程组的解为坐标的点在第四象限的概率.
|
(I)求方程组有解的概率;
(Ⅱ)求以方程组的解为坐标的点在第四象限的概率.
考点:列举法计算基本事件数及事件发生的概率
专题:概率与统计
分析:(Ⅰ)利用分布计数原理求出骰子投掷2次所有的结果,通过解二元一次方程组判断出方程组有唯一解的条件,求出满足该条件的结果个数,利用古典概型的概率公式求出方程组只有一个解的概率;
(Ⅱ)解方程组
,根据条件确定a,b的范围,从而确定满足该条件的结果个数利用古典概型的概率公式求出方程组只有一个解的概率.
(Ⅱ)解方程组
|
解答:
解:(Ⅰ)由题意知,基本事件空间Ω={(1,1),(1,2),(1,3),(1,4),
(1,5),(1,6),(2,1),(2,2),(2,3),(2,4),(2,5),(2,6),
…,(6,1),(6,2),(6,3),(6,4),(6,5),(6,6)},
基本事件总数n=36个,设A=“方程组有解”,则
=“方程组无解”.
若方程没有解,则
=
,即b=2a,
则符合条件的数组为(1,2),(2,4),(3,6),
所以P(
)=
=
,P(A)=1-
=
.
故方程组有解的概率为
.
(Ⅱ)由方程组
,
得
,
若b>2a,则有
,
即a=2,3,4,5,6,b=4,5,6,
符合条件的数组有(2,5),(2,6)共有2个,
若b<2a,则有
,
即b=1,2,a=1
符合条件的数组有(1,1)共1个,
∴概率为p=
=
,
即以方程组的解为坐标的点在第四象限的概率为
.
(1,5),(1,6),(2,1),(2,2),(2,3),(2,4),(2,5),(2,6),
…,(6,1),(6,2),(6,3),(6,4),(6,5),(6,6)},
基本事件总数n=36个,设A=“方程组有解”,则
. |
| A |
若方程没有解,则
| a |
| 1 |
| b |
| 2 |
则符合条件的数组为(1,2),(2,4),(3,6),
所以P(
. |
| A |
| 3 |
| 36 |
| 1 |
| 12 |
| 1 |
| 12 |
| 11 |
| 12 |
故方程组有解的概率为
| 11 |
| 12 |
(Ⅱ)由方程组
|
得
|
若b>2a,则有
|
即a=2,3,4,5,6,b=4,5,6,
符合条件的数组有(2,5),(2,6)共有2个,
若b<2a,则有
|
即b=1,2,a=1
符合条件的数组有(1,1)共1个,
∴概率为p=
| 1+2 |
| 36 |
| 1 |
| 12 |
即以方程组的解为坐标的点在第四象限的概率为
| 1 |
| 12 |
点评:本题考查古典概型及其概率计算公式的应用,属中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知函数f(x)=
若数列{an}满足an=f(n)(n∈N+),且{an}是递增数列,则实数a的取值范围是( )
|
A、[
| ||
B、(
| ||
| C、(2,3) | ||
| D、(1,3) |
设F为双曲线
-
=1(a>0,b>0)的右焦点,若双曲线与渐近线在第一象限分别存在点PQ.使得P为QF的中点,则双曲线离心率的取值范围为( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、(1,2) | ||
| B、(2,+∞ | ||
C、(1,
| ||
D、(
|
 某商场根据甲、乙两种不同品牌的洗衣粉在周一至周五每天的销量绘成如图所示的茎叶图,若两种品牌销量的平均数为
某商场根据甲、乙两种不同品牌的洗衣粉在周一至周五每天的销量绘成如图所示的茎叶图,若两种品牌销量的平均数为. |
| x甲 |
. |
| x乙 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
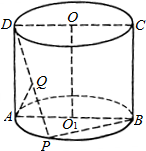 如图,圆柱OO1的底面圆半径为2,ABCD为经过圆柱轴OO1的截面,点P在
如图,圆柱OO1的底面圆半径为2,ABCD为经过圆柱轴OO1的截面,点P在
