题目内容
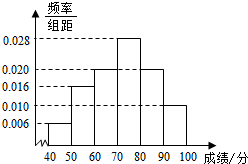 某校高三文科(1)班学生参加“江南十校”联考,其数学成绩(已折合成百分制)的频率分布直方图如图所示,其中成绩分布敬意为[40,50),[50,60),[60,70),[70,80),[80,90),[90,100],现已知成绩落在[90,100]的有5人.
某校高三文科(1)班学生参加“江南十校”联考,其数学成绩(已折合成百分制)的频率分布直方图如图所示,其中成绩分布敬意为[40,50),[50,60),[60,70),[70,80),[80,90),[90,100],现已知成绩落在[90,100]的有5人.(Ⅰ)求该校高三文科(1)班参加“江南十校”联考的总人数;
(Ⅱ)根据频率分布直方图,估计该班此次数学成绩的平均分(可用中值代替各组数据的平均值);
(Ⅲ)现要求从成绩在[40,50)和[90,100]的学生共选2人参加某项座谈会,求2人来自于同一分数段的概率.
考点:古典概型及其概率计算公式,频率分布直方图,众数、中位数、平均数
专题:概率与统计
分析:(I)成绩落在[90,100]的有5人,频率不0.010×10,由此能求出该校高三文科(1)班参加“江南十校”联考的总人数.
(II)利用频率分布直方图能求出平均分.
(Ⅲ) 成绩在[40,50)中共有0.006×10×50=3人,成绩在[90,100)中共有0.010×10×50=5人,要求从成绩在[40,50)和[90,100]的学生共选2人参加某项座谈会,总的基本事件有n=
=28个,其中2人来自同一分数段的基本事件有m=
+
=13个,由此能求出2人来自于同一分数段的概率.
(II)利用频率分布直方图能求出平均分.
(Ⅲ) 成绩在[40,50)中共有0.006×10×50=3人,成绩在[90,100)中共有0.010×10×50=5人,要求从成绩在[40,50)和[90,100]的学生共选2人参加某项座谈会,总的基本事件有n=
| C | 2 8 |
| C | 2 3 |
| C | 2 5 |
解答:
解:(I)该校高三文科(1)班参加“江南十校”联考的总人数为
=50(人).
(II)平均分
=45×0.06+55×0.16+65×0.20+75×0.28+85×0.20+95×0.10=72分.
(Ⅲ) 成绩在[40,50)中共有0.006×10×50=3人,
成绩在[90,100)中共有0.010×10×50=5人,
要求从成绩在[40,50)和[90,100]的学生共选2人参加某项座谈会,
总的基本事件有n=
=28个,
其中2人来自同一分数段的基本事件有m=
+
=13个,
∴2人来自于同一分数段的概率p=
=
.
| 5 |
| 0.010×10 |
(II)平均分
. |
| x |
(Ⅲ) 成绩在[40,50)中共有0.006×10×50=3人,
成绩在[90,100)中共有0.010×10×50=5人,
要求从成绩在[40,50)和[90,100]的学生共选2人参加某项座谈会,
总的基本事件有n=
| C | 2 8 |
其中2人来自同一分数段的基本事件有m=
| C | 2 3 |
| C | 2 5 |
∴2人来自于同一分数段的概率p=
| m |
| n |
| 13 |
| 28 |
点评:本题考查频率分布直方图的应用,考查概率的求法,是基础题,解题时要注意等可能事件概率计算公式的合理运用.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
执行如图所示的程序框图,若输入x=-1,则输入y的值为( )
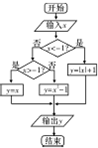

| A、-1 | B、0 | C、1 | D、2 |
若函数f(x)=
在其定义域上只有一个零点,则实数a的取值范围是( )
|
| A、a>16 | B、a≥16 |
| C、a<16 | D、a≤16 |
已知数列{an}满足a1=1,且anan+1=2n,则数列{an}的前20项的和为( )
| A、3×211-3 |
| B、3×211-1 |
| C、3×210-2 |
| D、3×210-5 |
由y=ex,x=0,y=2所围成的曲边梯形的面积为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
设变量x,y满足约束条件
,则z=2x-2y的取值范围为( )
|
| A、[4,32] | ||
B、[
| ||
| C、[8,16] | ||
D、[
|