题目内容
已知α的终边过点(-1,-2);
(1)求cosα及tanα的值.
(2)化简并求
的值.
(1)求cosα及tanα的值.
(2)化简并求
sin(π-α)cos(2π-α)sin(-α+
| ||
| tan(-α-π)sin(-π-α) |
考点:运用诱导公式化简求值,任意角的三角函数的定义
专题:三角函数的求值
分析:(1)首先,确定|OP|=
=
,(设P(-1,-2),O(0,0)),然后,结合三角函数的概念进行求解;
(2)先利用诱导公式化简给定的式子,然后,利用(1)的结果代入即可求解其值.
| (-1)2+(-2)2 |
| 5 |
(2)先利用诱导公式化简给定的式子,然后,利用(1)的结果代入即可求解其值.
解答:
解:(1)设P(-1,-2),O(0,0),
∴|OP|=
=
,
∴cosα=
=-
,
tanα=
=2,
∴cosα=-
,tanα=2.
(2)
=
=
=
=
,
∴
的值
.
∴|OP|=
| (-1)2+(-2)2 |
| 5 |
∴cosα=
| -1 | ||
|
| ||
| 5 |
tanα=
| -2 |
| -1 |
∴cosα=-
| ||
| 5 |
(2)
sin(π-α)cos(2π-α)sin(-α+
| ||
| tan(-α-π)sin(-π-α) |
=
| sinα•cosα•(-cosα) |
| -tanα•sinα |
=
| cos2α |
| tanα |
=
(-
| ||||
| 2 |
| 1 |
| 10 |
∴
sin(π-α)cos(2π-α)sin(-α+
| ||
| tan(-α-π)sin(-π-α) |
| 1 |
| 10 |
点评:本题重点考查了诱导公式及其运用,三角函数的定义等知识,属于中档题.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
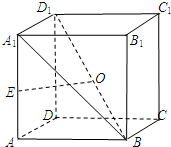 如图,在正方体ABCD-A1B1C1D1中,AA1=2,E为AA1的中点,O为BD1的中点.
如图,在正方体ABCD-A1B1C1D1中,AA1=2,E为AA1的中点,O为BD1的中点. 如图,已知AB是圆O的直径,圆O交BC于D,过点D作圆O的切线DE交AC于点E,且DE⊥AC.求证:AC=2OD.
如图,已知AB是圆O的直径,圆O交BC于D,过点D作圆O的切线DE交AC于点E,且DE⊥AC.求证:AC=2OD.