题目内容
若函数f(x)=(sinx+cosx)2+2cos2x-m在[0,
]上有零点,则m的取值范围为 .
| π |
| 2 |
考点:三角函数中的恒等变换应用,三角函数的周期性及其求法
专题:三角函数的求值,三角函数的图像与性质
分析:先利用两角和公式和二倍角公式对函数解析式化简整理,要使f(x)在[0,
]上有零点,需f(x)=0,进而得出
sin(2x+
)=m-2,利用x的范围求得m的范围.
| π |
| 2 |
| 2 |
| π |
| 4 |
解答:
解:f(x)=(sinx+cosx)2+2cos2x-m
=1+2sinxcosx+2cos2x-m
=sin2x+cos2x+2-m
=
sin(2x+
)+2-m,
要使f(x)在[0,
]上有零点,需f(x)=0,
即
sin(2x+
)+2-m=0
∴
sin(2x+
)=m-2,
∵x∈[0,
],
∴
≤2x+
≤
,
∴-1≤m-2≤
,
∴1≤m≤2+
,
故答案为:[1,2+
]
=1+2sinxcosx+2cos2x-m
=sin2x+cos2x+2-m
=
| 2 |
| π |
| 4 |
要使f(x)在[0,
| π |
| 2 |
即
| 2 |
| π |
| 4 |
∴
| 2 |
| π |
| 4 |
∵x∈[0,
| π |
| 2 |
∴
| π |
| 4 |
| π |
| 4 |
| 5π |
| 4 |
∴-1≤m-2≤
| 2 |
∴1≤m≤2+
| 2 |
故答案为:[1,2+
| 2 |
点评:本题主要考查了三角函数恒等变换的应用,三角函数图象与性质.解题的过程中注意数形结合思想和整体还原思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
复数(
)3的共轭复数为( )
| 1+i |
| 1-i |
| A、1 | B、-1 | C、i | D、-i |
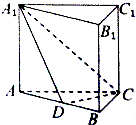 如图,三棱柱ABC-A1B1C1中,底面是边长为2的正三角形,侧棱AA1⊥底面ABC,D为AB的中点,且A1D与底面ABC所成角的正切值为2,则三棱锥A1-ACD外接球的表面积为
如图,三棱柱ABC-A1B1C1中,底面是边长为2的正三角形,侧棱AA1⊥底面ABC,D为AB的中点,且A1D与底面ABC所成角的正切值为2,则三棱锥A1-ACD外接球的表面积为