题目内容
已知圆O的弦CD与直径AB垂直并交于点F,点E在CD上,且AE=CE.
(1)求证:CA2=CE•CD;
(2)已知CD=5,AE=3,求sin∠EAF.
(1)求证:CA2=CE•CD;
(2)已知CD=5,AE=3,求sin∠EAF.
考点:与圆有关的比例线段
专题:选作题,立体几何
分析:(1)由⊙O的弦CD与直径AB垂直于F,根据垂径定理,易证得∠C=∠D,又由AE=CE,根据等边对等角,可得∠C=∠CAE,即可得∠CAE=∠D,又由∠C是公共角,即可证得△CEA∽△CAD,然后由相似三角形的对应边成比例,证得结论;
(2)求出DE,可得EF,在Rt△AFE中,求sin∠EAF.
(2)求出DE,可得EF,在Rt△AFE中,求sin∠EAF.
解答:
 (1)证明:在△CEA和△CAD中,
(1)证明:在△CEA和△CAD中,
∵弦CD⊥直径AB,
∴
=
,
∴∠D=∠C,
又∵AE=EC,
∴∠CAE=∠C,
∴∠CAE=∠D,
∵∠C是公共角,
∴△CEA∽△CAD,
∴
=
,
即CA2=CE•CD;
(2)解:∵CD=5,AE=CE=3,
∴DE=2,
∴EF=DF-DE=0.5,
在Rt△AFE中,sin∠EAF=
=
.
 (1)证明:在△CEA和△CAD中,
(1)证明:在△CEA和△CAD中,∵弦CD⊥直径AB,
∴
 |
| AC |
 |
| AD |
∴∠D=∠C,
又∵AE=EC,
∴∠CAE=∠C,
∴∠CAE=∠D,
∵∠C是公共角,
∴△CEA∽△CAD,
∴
| CA |
| CD |
| CE |
| CA |
即CA2=CE•CD;
(2)解:∵CD=5,AE=CE=3,
∴DE=2,
∴EF=DF-DE=0.5,
在Rt△AFE中,sin∠EAF=
| 0.5 |
| 3 |
| 1 |
| 6 |
点评:此题考查了相似三角形的判定与性质、垂径定理、等腰三角形的性质以及三角函数的定义

练习册系列答案
相关题目

 函数y=Asin(ωx+φ)(A>0,ω>0,0<φ<π)在一个周期内的图象如图,
函数y=Asin(ωx+φ)(A>0,ω>0,0<φ<π)在一个周期内的图象如图,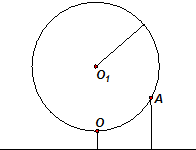 如图,某大风车的半径为2m,每12s逆时针旋转一周,它的最低点O离地面0.5m.风车圆周上一点A从最低点O开始,运动t(s)后与地面的距离为f(t).
如图,某大风车的半径为2m,每12s逆时针旋转一周,它的最低点O离地面0.5m.风车圆周上一点A从最低点O开始,运动t(s)后与地面的距离为f(t).