题目内容
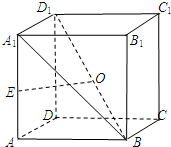 如图,在正方体ABCD-A1B1C1D1中,AA1=2,E为AA1的中点,O为BD1的中点.
如图,在正方体ABCD-A1B1C1D1中,AA1=2,E为AA1的中点,O为BD1的中点.(Ⅰ)求证:平面A1BD1⊥平面ABB1A1;
(Ⅱ)求证:EO∥平面ABCD;
(Ⅲ)设P为正方体ABCD-A1B1C1D1棱上一点,给出满足条件OP=
| 2 |
考点:平面与平面垂直的判定,直线与平面平行的判定
专题:圆锥曲线的定义、性质与方程
分析:(Ⅰ)在正方体ABCD-A1B1C1D1中,因为 A1D1⊥平面ABB1A1,A1D1?平面A1BD1,利用面面垂直的性质推断出平面A1BD1⊥平面ABB1A1.
(Ⅱ)连接BD,AC,设BD∩AC=G,连接0G.因 为ABCD-A1B1C1D1为正方体,进而可知 AE∥DD1,且AE=
DD1,且G是BD的中点,又因为O是BD1的中点,
所以 OG∥DD1,且OG=
DD1,所以 OG∥AE,且OG=AE,即四边形AGOE是平行四边形,所以OE∥AG,又因为 EO?平面ABCD,AG?平面ABCD.所以EO∥平面ABCD.
(Ⅲ)解:因根据ABCD-A1B1C1D1为正方体,AA1=2,所以 求得AC=,所以求得 OE=AG.在正方体ABCD-A1B1C1D1中,因为 AA1⊥平面ABCD,AG?平面ABCD,
判断出 AA1⊥AG,又因为 EO∥AG,所以 AA1⊥OE,则点O到棱AA1的距离为,所以在棱AA1上有且只有一个点(即中点E)到点O的距离等于,同理,正方体ABCD-A1B1C1D1每条棱的中点到点的距离都等于,在正方体ABCD-A1B1C1D1棱上使得OP=
的点P有12个.所以在正方体ABCD-A1B1C1D1棱上使得OP=
的点P有12个.
(Ⅱ)连接BD,AC,设BD∩AC=G,连接0G.因 为ABCD-A1B1C1D1为正方体,进而可知 AE∥DD1,且AE=
| 1 |
| 2 |
所以 OG∥DD1,且OG=
| 1 |
| 2 |
(Ⅲ)解:因根据ABCD-A1B1C1D1为正方体,AA1=2,所以 求得AC=,所以求得 OE=AG.在正方体ABCD-A1B1C1D1中,因为 AA1⊥平面ABCD,AG?平面ABCD,
判断出 AA1⊥AG,又因为 EO∥AG,所以 AA1⊥OE,则点O到棱AA1的距离为,所以在棱AA1上有且只有一个点(即中点E)到点O的距离等于,同理,正方体ABCD-A1B1C1D1每条棱的中点到点的距离都等于,在正方体ABCD-A1B1C1D1棱上使得OP=
| 2 |
| 2 |
解答:
(Ⅰ)证明:在正方体ABCD-A1B1C1D1中,
∵A1D1⊥平面ABB1A1,A1D1?平面A1BD1,
∴平面A1BD1⊥平面ABB1A1.
(Ⅱ)证明:连接BD,AC,设BD∩AC=G,连接0G.
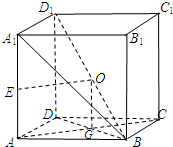
∵ABCD-A1B1C1D1为正方体,
∴AE∥DD1,且AE=
DD1,且G是BD的中点,
又因为O是BD1的中点,
∴OG∥DD1,且OG=
DD1,
∴OG∥AE,且OG=AE,
即四边形AGOE是平行四边形,
所以OE∥AG,
又∵EO?平面ABCD,AG?平面ABCD,
所以EO∥平面ABCD.
(Ⅲ)解:满足条件OP=
的点P有12个.
理由如下:
因为 ABCD-A1B1C1D1为正方体,AA1=2,
所以 AC=2
.
所以 OE=AG=
AC=
.
在正方体ABCD-A1B1C1D1中,
因为 AA1⊥平面ABCD,AG?平面ABCD,
所以 AA1⊥AG,
又因为 EO∥AG,
所以 AA1⊥OE,
则点O到棱AA1的距离为
,
所以在棱AA1上有且只有一个点(即中点E)到点O的距离等于
,
同理,正方体ABCD-A1B1C1D1每条棱的中点到点的距离都等于
,
所以在正方体ABCD-A1B1C1D1棱上使得OP=
的点P有12个.
∵A1D1⊥平面ABB1A1,A1D1?平面A1BD1,
∴平面A1BD1⊥平面ABB1A1.
(Ⅱ)证明:连接BD,AC,设BD∩AC=G,连接0G.

∵ABCD-A1B1C1D1为正方体,
∴AE∥DD1,且AE=
| 1 |
| 2 |
又因为O是BD1的中点,
∴OG∥DD1,且OG=
| 1 |
| 2 |
∴OG∥AE,且OG=AE,
即四边形AGOE是平行四边形,
所以OE∥AG,
又∵EO?平面ABCD,AG?平面ABCD,
所以EO∥平面ABCD.
(Ⅲ)解:满足条件OP=
| 2 |
理由如下:
因为 ABCD-A1B1C1D1为正方体,AA1=2,
所以 AC=2
| 2 |
所以 OE=AG=
| 1 |
| 2 |
| 2 |
在正方体ABCD-A1B1C1D1中,
因为 AA1⊥平面ABCD,AG?平面ABCD,
所以 AA1⊥AG,
又因为 EO∥AG,
所以 AA1⊥OE,
则点O到棱AA1的距离为
| 2 |
所以在棱AA1上有且只有一个点(即中点E)到点O的距离等于
| 2 |
同理,正方体ABCD-A1B1C1D1每条棱的中点到点的距离都等于
| 2 |
所以在正方体ABCD-A1B1C1D1棱上使得OP=
| 2 |
点评:本题主要考查了线面平行,线面垂直的判定定理.考查了学生分析推理的能力.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
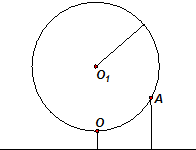 如图,某大风车的半径为2m,每12s逆时针旋转一周,它的最低点O离地面0.5m.风车圆周上一点A从最低点O开始,运动t(s)后与地面的距离为f(t).
如图,某大风车的半径为2m,每12s逆时针旋转一周,它的最低点O离地面0.5m.风车圆周上一点A从最低点O开始,运动t(s)后与地面的距离为f(t).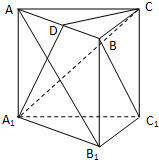 如图,已知直三棱柱ABC-A1B1C1中,AC⊥BC,D为AB的中点,AC=BC=BB1.
如图,已知直三棱柱ABC-A1B1C1中,AC⊥BC,D为AB的中点,AC=BC=BB1.