题目内容
正项数列{an}满足:它的平方数列{an2}是公差为1,第4项为4的等差数列.
(1)求数列{an}的通项公式;
(2)若数列bn=
的前n项和为Sn,求Sn.
(1)求数列{an}的通项公式;
(2)若数列bn=
| 1 |
| an+1+an |
考点:数列的求和,等差数列的性质
专题:等差数列与等比数列
分析:(1)根据条件确定a1,构造等差数列即可求数列{an}的通项公式;
(2)求出bn的通项公式,利用分母有理化,进行求和.
(2)求出bn的通项公式,利用分母有理化,进行求和.
解答:
解:(1)∵数列{an2}是公差为1,第4项为4的等差数列,
∴a42=a12+(4-1)×1=4,即a12=1,
即数列{
}是以1为首项,1为公差的等差数列,则
=1+(n-1)=n,
即an=±
.
∵正项数列{an},
∴an=
.
(2)bn=
=
=
-
,
则Sn=(
-1)+(
-
)+…+
-
=
-1.
∴a42=a12+(4-1)×1=4,即a12=1,
即数列{
| a | 2 n |
| a | 2 n |
即an=±
| n |
∵正项数列{an},
∴an=
| n |
(2)bn=
| 1 |
| an+1+an |
| 1 | ||||
|
| n+1 |
| n |
则Sn=(
| 2 |
| 3 |
| 2 |
| n+1 |
| n |
| n+1 |
点评:本题主要考查等差数列的通项公式,以及利用分母有理化进行数列求和,考查学生的计算能力.

练习册系列答案
相关题目
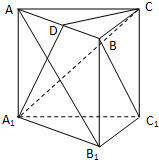 如图,已知直三棱柱ABC-A1B1C1中,AC⊥BC,D为AB的中点,AC=BC=BB1.
如图,已知直三棱柱ABC-A1B1C1中,AC⊥BC,D为AB的中点,AC=BC=BB1.