题目内容
设等差数列{an}的公差d=3,前n项的和为Sn,则
= .
| lim |
| n→∞ |
| 2an2-n2+1 |
| Sn |
考点:极限及其运算
专题:计算题
分析:设出等差数列的首项,把通项与前n项和用首项和n表示,整理后分子分母同时除以n2再求极限.
解答:
解:设等差数列{an}的首项为a1,
又公差d=3,
则an=a1+3(n-1),sn=na1+
=
n,
∴
=
•2
=
2•
=2•
=
.
故答案为:
.
又公差d=3,
则an=a1+3(n-1),sn=na1+
| 3n(n-1) |
| 2 |
| 2a1+3n-3 |
| 2 |
∴
| lim |
| n→∞ |
| 2an2-n2+1 |
| Sn |
| lim |
| n→∞ |
| (2a1+6n-6)2-n2+1 |
| (2a1+3n-3)n |
=
| lim |
| n→∞ |
(
| ||||
|
| (0+6)2-1+0 |
| 0+3 |
| 70 |
| 3 |
故答案为:
| 70 |
| 3 |
点评:本题考查了极限及其运算,考查了等差数列的通项公式和前n项和公式,考查了计算能力,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
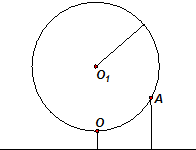 如图,某大风车的半径为2m,每12s逆时针旋转一周,它的最低点O离地面0.5m.风车圆周上一点A从最低点O开始,运动t(s)后与地面的距离为f(t).
如图,某大风车的半径为2m,每12s逆时针旋转一周,它的最低点O离地面0.5m.风车圆周上一点A从最低点O开始,运动t(s)后与地面的距离为f(t).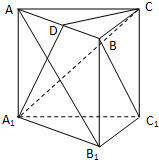 如图,已知直三棱柱ABC-A1B1C1中,AC⊥BC,D为AB的中点,AC=BC=BB1.
如图,已知直三棱柱ABC-A1B1C1中,AC⊥BC,D为AB的中点,AC=BC=BB1. 如图,D为△ABC的边BC中点,E在AC上且AE=3,EC=2,AD交BE于F,那么
如图,D为△ABC的边BC中点,E在AC上且AE=3,EC=2,AD交BE于F,那么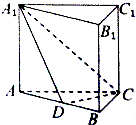 如图,三棱柱ABC-A1B1C1中,底面是边长为2的正三角形,侧棱AA1⊥底面ABC,D为AB的中点,且A1D与底面ABC所成角的正切值为2,则三棱锥A1-ACD外接球的表面积为
如图,三棱柱ABC-A1B1C1中,底面是边长为2的正三角形,侧棱AA1⊥底面ABC,D为AB的中点,且A1D与底面ABC所成角的正切值为2,则三棱锥A1-ACD外接球的表面积为