题目内容
如图，已知AB是圆O的直径，圆O交BC于D，过点D作圆O的切线DE交AC于点E，且DE⊥AC．求证：AC=2OD．考点：与圆有关的比例线段
专题：选作题,立体几何
分析：连接OD，证明OD∥AC，利用OD是△ABC的中位线，即可得出结论．
解答：
证明：连接OD，则
∵DE是圆O的切线，
∴OD⊥DE，
∵DE⊥AC，
∴OD∥AC，
∵O是AB的中点，
∴OD是△ABC的中位线，
∴OD=
AC，
∴AC=2OD．
证明：连接OD，则∵DE是圆O的切线，
∴OD⊥DE，
∵DE⊥AC，
∴OD∥AC，
∵O是AB的中点，
∴OD是△ABC的中位线，
∴OD=
| 1 |
| 2 |
∴AC=2OD．
点评：本题考查圆的切线的性质，考查三角形中位线的性质，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
如图，已知直三棱柱ABC-A1B1C1中，AC⊥BC，D为AB的中点，AC=BC=BB1．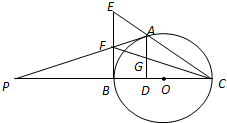
如图，A是以BC为直径的⊙O上一点，AD⊥BC于点D，过点B作⊙O的切线，与CA的延长线相交于点E，G是AD的中点，连结CG并延长与BE相交于点F，延长AF与CB的延长线相交于点P．
如图，D为△ABC的边BC中点，E在AC上且AE=3，EC=2，AD交BE于F，那么