Question

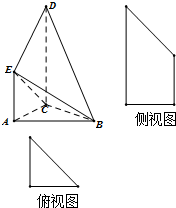如图是某直三棱柱（侧棱与底面垂直）被削去一部分后的直观图与三视图中的侧（左）视图、俯视图，侧（左）视图是底边长分别为2和4的直角梯形，俯视图是直角边长为2的等腰直角三角形．
（Ⅰ）求出该几何体的体积；
（Ⅱ）求证：平面BDE⊥平面BCD；
（Ⅲ）求直线CE与平面BDE的夹角正弦值．

Answer 1

考点：平面与平面垂直的判定,由三视图求面积、体积,直线与平面所成的角

专题：综合题,空间位置关系与距离,空间角

分析：（Ⅰ）证明AB⊥平面ACDE，即可求出四棱锥B-ACDE的体积；
（Ⅱ）以A为原点建立空间直角坐标系，求出平面BDE和平面BCD的法向量，证明其数量积为0，即可证明平面BDE⊥平面BCD；
（Ⅲ）利用向量的夹角公式，即可求直线CE与平面BDE的夹角正弦值．

解答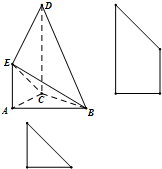： （Ⅰ）解：由题意可知，四棱锥B-ACDE中，
AE⊥平面ABC，∴AE⊥AB，
又AB⊥AC，且AE和AC相交，
∴AB⊥平面ACDE，
又AC=AB=AE=2，CD=4，
则四棱锥B-ACDE的体积为V=

1

3

SACDE•AB=

1

3

×

(4+2)×2

2

×2=4．…（4分）
（Ⅱ）证明：如图，以A为原点建立空间直角坐标系，
∴B（2，0，0），C（0，2，0），E（0，0，2），D（0，2，4）

BE

=(-2，0，2)，

DE

=(0，-2，-2)

BC

=(-2，2，0)，

CD

=(0，0，4)…（5分）
设平面BDE和平面BCD的法向量分别为

m

=(x1，y1，z1)，

n

=(x2，y2，z2)

m

•

BE

=-2x1+2z1=0，

m

•

DE

=-2y1-2z1=0，取

m

=(1，-1，1)…（6分）

n

•

BC

=-2x₂+2y₂=0，

n

•

CD

=4z₂=0，取

n

=（1，1，0）…（7分）
∵

m

•

n

=1-1+0=0，∴

m

⊥

n

，
∴平面BDE⊥平面BCD           …（8分）
（Ⅲ）解：

CE

=(0，-2，2)，
∴cos＜

m

，

CE

＞=

2+2

3 • 8

=

6

3

…（11分）
直线CE与平面BDE的夹角正弦值为

6

3

…（12分）

点评：本题考查几何体的体积、面面垂直考查线面角，考查向量知识的运用，考查学生分析解决问题的能力，难度中等．