题目内容
在平面直角坐标系xoy中,已知椭圆C:
+
=1(a>b>0)的左、右焦点分别F1、F2焦距为2,且与双曲线
-y2=1共顶点.P为椭圆C上一点,直线PF1交椭圆C于另一点Q.
(1)求椭圆C的方程;
(2)若点P的坐标为(0,b),求过P、Q、F2三点的圆的方程;
(3)若
=λ
,且λ∈[
,2],求
•
的最大值.
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| 2 |
(1)求椭圆C的方程;
(2)若点P的坐标为(0,b),求过P、Q、F2三点的圆的方程;
(3)若
| F1P |
| QF1 |
| 1 |
| 2 |
| OP |
| OQ |
考点:直线与圆锥曲线的关系,平面向量数量积的运算,圆的标准方程,椭圆的标准方程
专题:综合题,直线与圆,圆锥曲线的定义、性质与方程
分析:(1)由题意得c=1,a2=2,可得椭圆C的方程;
(2)先求出点Q的坐标,再利用待定系数法,即可求过P、Q、F2三点的圆的方程;
(3)利用
=λ
,结合向量的数量积公式,结合基本不等式,即可求
•
的最大值.
(2)先求出点Q的坐标,再利用待定系数法,即可求过P、Q、F2三点的圆的方程;
(3)利用
| F1P |
| QF1 |
| OP |
| OQ |
解答:
解:(1)由题意得c=1,a2=2…(2分)
故椭圆的方程为
+y2=1.…(3分)
(2)因为P(0,1),F1(-1,0),所以PF1的方程为x-y+1=0
由
,解得点Q的坐标为(-
,-
). …(5分)
设过P,Q,F2三点的圆为x2+y2+Dx+Ey+F=0…(6分)
则
解得D=
,E=
,F=-
所以圆的方程为x2+y2+
x+
y-
=0…(8分)
(3)设P(x1,y1),Q(x2,y2),则
=(x1+1,y1),
=(-1-x2,-y2)
因为
=λ
,所以
,即
所以
,解得x2=
…(10分)
所以
•
=x1x2+y1y2=x2(-λx2-λ-1)-λ
=-
-(1+λ)x2-λ
=-
(
)2-(1+λ)•
-λ=
-
(λ+
)…(12分)
因为λ∈[
,2],所以λ+
≥2,当且仅当λ=
,
即λ=1时,取等号.
•
最大值为
. …(14分)
故椭圆的方程为
| x2 |
| 2 |
(2)因为P(0,1),F1(-1,0),所以PF1的方程为x-y+1=0
由
|
| 4 |
| 3 |
| 1 |
| 3 |
设过P,Q,F2三点的圆为x2+y2+Dx+Ey+F=0…(6分)
则
|
| 1 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
所以圆的方程为x2+y2+
| 1 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
(3)设P(x1,y1),Q(x2,y2),则
| F1P |
| QF1 |
因为
| F1P |
| QF1 |
|
|
所以
|
| 1-3λ |
| 2λ |
所以
| OP |
| OQ |
| y | 2 2 |
| λ |
| 2 |
| x | 2 2 |
=-
| λ |
| 2 |
| 1-3λ |
| 2λ |
| 1-3λ |
| 2λ |
| 7 |
| 4 |
| 5 |
| 8 |
| 1 |
| λ |
因为λ∈[
| 1 |
| 2 |
| 1 |
| λ |
| 1 |
| λ |
即λ=1时,取等号.
| OP |
| OQ |
| 1 |
| 2 |
点评:本题考查椭圆的方程,考查圆的方程,考查向量知识的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
已知向量
=(2,1),
=(3,4),则向量
在向量
方向上正射影的数量为( )
| a |
| b |
| a |
| b |
| A、-2 | ||
| B、2 | ||
C、
| ||
| D、5 |
现有60件产品,编号从1到60,若用系统抽样方法从中抽取6件检验,则所抽到的个体编号可能是( )
| A、5,10,15,20,25,30 |
| B、2,14,26,28,42,56 |
| C、5,8,31,36,48,54 |
| D、3,13,23,33,43,53 |
已知2a+1<0,关于x的不等式x2-4ax-5a2>0的解集是( )
| A、{x|x>5a或x<-a} |
| B、{x|-a<x<5a} |
| C、{x|x<5a或x>-a} |
| D、{x|5a<x<-a} |
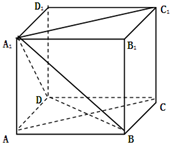
如图,在正方体ABCD-A1B1C1D1中,下列结论不正确的是( )


| A、C1D1⊥B1C |
| B、BD1⊥AC |
| C、BD1∥B1C |
| D、∠ACB1=60° |
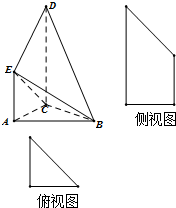 如图是某直三棱柱(侧棱与底面垂直)被削去一部分后的直观图与三视图中的侧(左)视图、俯视图,侧(左)视图是底边长分别为2和4的直角梯形,俯视图是直角边长为2的等腰直角三角形.
如图是某直三棱柱(侧棱与底面垂直)被削去一部分后的直观图与三视图中的侧(左)视图、俯视图,侧(左)视图是底边长分别为2和4的直角梯形,俯视图是直角边长为2的等腰直角三角形.