题目内容
若数列{an}满足a1=2且an+an-1=2n+2n-1，Sn为数列{an}的前n项和，则log2（S2012+2）等于（ ）
| A、2013 | B、2012 |
| C、2011 | D、2010 |
考点：数列递推式,数列的求和
专题：等差数列与等比数列
分析：求出数列的通项公式和前n项和，结合对数的基本运算即可得到结论．
解答：
解：∵an+an-1=2n+2n-1，
∴an=2n，即数列{an}是公比q=2的等比数列，
则Sn=
=2n+1-2，
则S2012=22013-2，
则log2（S2012+2）=log222013=2013，
故选：A．
∴an=2n，即数列{an}是公比q=2的等比数列，
则Sn=
| 2•(1-2n) |
| 1-2 |
则S2012=22013-2，
则log2（S2012+2）=log222013=2013，
故选：A．
点评：本题主要考查对数的基本运算，根据条件求出数列的通项公式以及数列的前n项和是解决本题的关键．
练习册系列答案
相关题目
设a，b是两条不同的直线，α，β是两个不同的平面，则（ ）
| A、若a∥α，b∥α，则a∥b |
| B、若a∥α，a∥β，则α∥β |
| C、若a∥b，a⊥α，则b⊥α |
| D、若a∥α，α⊥β，则α⊥β |
已知向量
=（2，1），
=（3，4），则向量
在向量
方向上正射影的数量为（ ）
| a |
| b |
| a |
| b |
| A、-2 | ||
| B、2 | ||
C、
| ||
| D、5 |
曲线y=
x3-2在点（1，-
） 处切线的斜率为（ ）
| 1 |
| 3 |
| 5 |
| 3 |
A、
| ||
| B、1 | ||
| C、-1 | ||
D、-
|
若复数z满足z=1-2i，则z的虚部为（ ）
| A、-2i | B、2i | C、-2 | D、2 |
现有60件产品，编号从1到60，若用系统抽样方法从中抽取6件检验，则所抽到的个体编号可能是（ ）
| A、5，10，15，20，25，30 |
| B、2，14，26，28，42，56 |
| C、5，8，31，36，48，54 |
| D、3，13，23，33，43，53 |
已知2a+1＜0，关于x的不等式x2-4ax-5a2＞0的解集是（ ）
| A、{x|x＞5a或x＜-a} |
| B、{x|-a＜x＜5a} |
| C、{x|x＜5a或x＞-a} |
| D、{x|5a＜x＜-a} |
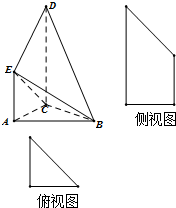如图是某直三棱柱（侧棱与底面垂直）被削去一部分后的直观图与三视图中的侧（左）视图、俯视图，侧（左）视图是底边长分别为2和4的直角梯形，俯视图是直角边长为2的等腰直角三角形．