题目内容

已知|
a
|=1，|
b
|=
2

（1）若
a
∥
b
，求
a
•
b
；
（2）若
a
，
b
的夹角为135°，求|
a
+
b
|；
（3）若
a
-
b
与
a
垂直，求
a
与
b
的夹角．
考点：平面向量数量积的运算
专题：平面向量及应用
分析：（1）由
a
∥
b
可得向量
a
，
b
的夹角θ为0°或180°，由数量积的定义可得；
（2）代入数据，由模长公式可得；（3）由垂直可得（
a
-
b
）•
a
=
a
2-
a
•
b
=0，可解夹角的余弦值，进而可得夹角．
解答： 解：（1）∵|
a
|=1，|
b
|=
2
，
a
∥
b
，
∴向量
a
，
b
的夹角θ为0°或180°，
∴
a
•
b
=|
a
||
b
|cos0°=
2
，
或
a
•
b
=|
a
||
b
|cos180°=-
2
；
（2）∵
a
，
b
的夹角为135°，
∴|
a
+
b
|=
(
a
+
b
)2
=
a
2+2
a
•
b
+
b
2

=
1+2×1×
2
×(-
2
2
)+2
=1；
（3）若
a
-
b
与
a
垂直，则（
a
-
b
）•
a

=
a
2-
a
•
b
=1-1×
2
×cos＜
a
，
b
＞=0，
解得cos＜
a
，
b
＞=
2
2
，
∴
a
与
b
的夹角为45°
点评：本题考查平面向量的基本运算，涉及模长公式以及平行与垂直，属基础题．
练习册系列答案
相关题目
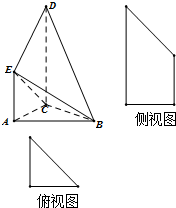如图是某直三棱柱（侧棱与底面垂直）被削去一部分后的直观图与三视图中的侧（左）视图、俯视图，侧（左）视图是底边长分别为2和4的直角梯形，俯视图是直角边长为2的等腰直角三角形．
（Ⅰ）求出该几何体的体积；
（Ⅱ）求证：平面BDE⊥平面BCD；
（Ⅲ）求直线CE与平面BDE的夹角正弦值．
已知A盒中有2个红球和2个黑球；B盒中有2个红球和3个黑球，现从A盒与B盒中各取一个球出来再放入对方盒中．
（1）求A盒中有2个红球的概率；
（2）求A盒中红球数ξ的分布列及数学期望．
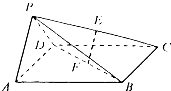如图，在四棱锥P-ABCD中，底面ABCD是正方形，侧面PAD⊥底面ABCD，且△PAD为等腰直角三角形，PA⊥PD，E、F分别为PC、BD的中点．
（Ⅰ）求证：EF∥平面PAD；
（Ⅱ）求证：平面PAB⊥平面PDC．
已知函数f（x）=x•（1+lnx），（x＞0）．
（Ⅰ）求函数f（x）的单调区间；
（Ⅱ）若k（x-2）＜f（x）对任意x≥32恒成立，求k的取值范围．
已知实数a，b满足|a|＜2，|b|＜2，证明：2|a+b|＜|4+ab|．
记Sn是数列{an}的前n项和，且Sn+an=2n+1（n∈N*）．
（1）求证：数列{an-2}是等比数列；
（2）求和：S1+S2+…+Sn．
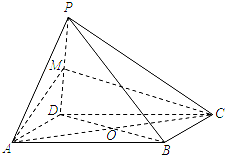如图，四棱锥P-ABCD中，O为菱形ABCD对角线的交点，M为棱PD的中点，MA=MC．
（1）求证：PB∥平面AMC；
（2）求证：平面PBD⊥平面AMC．
如图，已知点P在正方体ABCD-A1B1C1D1的对角线BD1上，∠PDA=60°．
（1）求DP与CC1所成角的大小；
（2）求DP与平面AA1D1D所成角的大小．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网