题目内容
函数f（x）=lnx的图象在点x=1处的切线方程是 ．
考点：椭圆的简单性质
专题：计算题,导数的概念及应用
分析：x=1代入解析式求出切点的坐标，再求出函数的导数后代入求出f′（1），即为所求的切线斜率，再代入点斜式进行整理即可．
解答：
解：把x=1代入f（x）=lnx得，f（1）=ln1=0，
∴切点的坐标为：（1，0），
由f′（x）=（lnx）′=
，得在点x=1处的切线斜率k=f′（1）=1，
∴在点x=1处的切线方程为：y=x-1，
故答案为：y=x-1．
∴切点的坐标为：（1，0），
由f′（x）=（lnx）′=
| 1 |
| x |
∴在点x=1处的切线方程为：y=x-1，
故答案为：y=x-1．
点评：本题考查了导数的几何意义和直线点斜式方程，关键求出某点处切线的斜率即该点处的导数值，还有切点的坐标，利用切点在曲线上和切线上．
练习册系列答案
相关题目
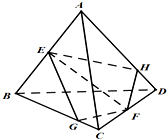如图，在四面体ABCD中，E，F分别为AB，CD的中点，过EF任作一个平面
