题目内容

若双曲线x2-
y2
b2
=1（b＞0）的一条渐近线与圆x2+（y-2）2=1至多有一个公共点，则双曲线离心率的取值范围是
 
．
考点：双曲线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：双曲线x2-
y2
b2
=1（b＞0）的一条渐近线与圆x2+（y-2）2=1至多有一个交点，可得圆心（0，2）到渐近线的距离≥半径r，解出即可．
解答： 解：圆x2+（y-2）2=1的圆心（0，2），半径r=1．
∵双曲线x2-
y2
b2
=1（b＞0）的一条渐近线与圆x2+（y-2）2=1至多有一个交点，
∴
2
b2+1
≥1，化为b2≤3．
∴e2=1+b2≤4，
∵e＞1，
∴1＜e≤2，
∴该双曲线的离心率的取值范围是（1，2]．
故答案为：（1，2]．
点评：熟练掌握双曲线的渐近线方程、离心率的计算公式、圆的标准方程、直线与圆的位置关系、点到直线的距离公式是解题的关键．
练习册系列答案
相关题目
已知幂函数f（x）=（m-1）2x m2-4m+2在（0，+∞）上单调递增，函数g（x）=2x-k．
（Ⅰ）求m的值；
（Ⅱ）当x∈[1，2]时，记f（x），g（x）的值域分别为集合A，B，若A∪B⊆A，求实数K的取值范围．
“a=2”是“直线ax+2y=0与直线x+y=1平行”的
 
条件．
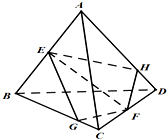如图，在四面体ABCD中，E，F分别为AB，CD的中点，过EF任作一个平面
α分别与直线BC，AD相交于点G，H，下列判断中：
①对于任意的平面α，都有S△EFG=S△EFH；
②存在一个平面α0，使得点G在线段BC上，点H在线段AD的延长线上；
③对于任意的平面α，都有直线GF，EH，BD相交于同一点或相互平行；
④对于任意的平面α，当G，H在线段BC，AD上时，几何体AC-EGFH的体积是一个定值．
其中正确的序号是（　　）
A、①③④B、③④
C、②③D、①②③
已知命题正确的个数是（　　）
①若
a
•
b
=0，则
a
=
0
或
b
=
0
；
②（
a
•
b
）•
c
=
a
•（
b
•
c
）；
③若
a
•
b
=
b
•
c
（
b
≠
0
），则
a
=
c
；
④
a
•
b
=
b
•
a
；
⑤若
a
与
b
不共线，则
a
与
b
的夹角为锐角．
A、1B、2C、3D、4
已知公比不为1的等比数列{an}的首项a1=
1
2
，前n项和为Sn，且a4+S4，a5+S5，a6+S6成等差数列．
（1）求等比数列{an}的通项公式；
（2）当n≥3时，求数列{|3+log2an|}的前n项和Tn．
已知函数f（x）=lnx-mx（m∈R），e为自然对数的底数．
（1）讨论函数f（x）在区间（e，+∞）上的单调性，并求出极值．
（2）若函数f（x）有两个不同的零点x1，x2，求证：x1x2＞e2．
若函数y=logax（a＞0，且a≠1）的图象如图所示，则下列函数图象正确的是（　　）
A、
B、
C、
D、
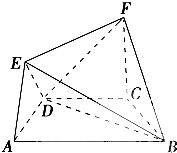在如图所示的几何体中，四边形ABCD是等腰梯形，AB∥CD，∠DAB=60°，FC⊥平面ABCD，AE⊥BD，CB=CD=CF=1，
（1）求证：BD⊥平面AED；
（2）求B到平面FDC的距离．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网