题目内容

函数y=2sin（2x-
π
6
）（x∈[0，π]）在下列哪个区间上单调递增（　　）
A、[
π
3
，
5π
6
]
B、[
π
12
，
7π
12
]
C、[0，
π
3
]
D、[0，π]
考点：正弦函数的图象
专题：三角函数的图像与性质
分析：根据正弦型函数的单调性，求出函数y=2sin（2x-
π
6
）（x∈[0，π]）的单调递区间，进而可得答案．
解答： 解：由2x-
π
6
∈[-
π
2
+2kπ，
π
2
+2kπ]，k∈Z得：
x∈[-
π
6
+kπ，
π
3
+2kπ]，k∈Z，
即函数y=2sin（2x-
π
6
）的单调递增区间为：[-
π
6
+kπ，
π
3
+2kπ]，k∈Z，
又∵x∈[0，π]，
故函数y=2sin（2x-
π
6
）（x∈[0，π]）在[0，
π
3
]和[
5π
6
，π]上单调递增，
故选：C
点评：本题主要考查两角和的余弦公式的应用，正弦函数的单调增区间，属于基础题．
练习册系列答案
相关题目
用数字1、2、3、4、5可组成没有重复数字的三位数共有（　　）
A、10个B、15个
C、60个D、125个
设a＞0，b＞0，求证：
a+b
2
-
ab
≥
a2+b2
2
-
a+b
2
．
设f（x）为定义在区间I上的函数．若对I上任意两点x1，x2（x1≠x2），总有f（
x1+x2
2
）＜
1
2
[f（x1）+f（x2）]，则称f（x）为I上的严格下凸函数．若f（x）为I上的严格下凸函数，其充要条件为：对任意x∈I有f″（x）＞0成立（f″（x）是函数f（x）导函数的导函数），则以下结论正确的有
 
．
①f（x）=
2x+2014
3x+7
，x∈[0，2014]是严格下凸函数．
②设x1，x2∈（0，
π
2
）且x1≠x2，则有tan（
x1+x2
2
）＞
1
2
（tanx1+tanx2）
③f（x）=-x3+3x2在区间[1，2014]上是严格下凸函数．
④f（x）=
1
6
x3+sinx，（x∈（
π
6
，
π
3
））是严格下凸函数．
“a=2”是“直线ax+2y=0与直线x+y=1平行”的
 
条件．
函数f（x）=2x-cosx，{an}是公差为
π
8
的等差数列，f（a1）+f（a2）+…+f（a7）=7π，则[f（a4）]2-a1a7=
 
．
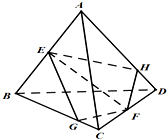如图，在四面体ABCD中，E，F分别为AB，CD的中点，过EF任作一个平面
α分别与直线BC，AD相交于点G，H，下列判断中：
①对于任意的平面α，都有S△EFG=S△EFH；
②存在一个平面α0，使得点G在线段BC上，点H在线段AD的延长线上；
③对于任意的平面α，都有直线GF，EH，BD相交于同一点或相互平行；
④对于任意的平面α，当G，H在线段BC，AD上时，几何体AC-EGFH的体积是一个定值．
其中正确的序号是（　　）
A、①③④B、③④
C、②③D、①②③
已知公比不为1的等比数列{an}的首项a1=
1
2
，前n项和为Sn，且a4+S4，a5+S5，a6+S6成等差数列．
（1）求等比数列{an}的通项公式；
（2）当n≥3时，求数列{|3+log2an|}的前n项和Tn．
i是虚数单位，复数（1-i）•（1+i）=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网