题目内容
设函数f(x)=
mx2-2x+lnx.
(Ⅰ)判断x=1能否为函数f(x)的极值点,并说明理由;
(Ⅱ)若m≥0,求f(x)的单调递增区间;
(Ⅲ)若存在m∈[-4,-1),使得定义在[1,t]上的函数g(x)=f(x)-ln(x+1)+x3在x=1处取得最大值,求实数t的最大值.
| 1 |
| 2 |
(Ⅰ)判断x=1能否为函数f(x)的极值点,并说明理由;
(Ⅱ)若m≥0,求f(x)的单调递增区间;
(Ⅲ)若存在m∈[-4,-1),使得定义在[1,t]上的函数g(x)=f(x)-ln(x+1)+x3在x=1处取得最大值,求实数t的最大值.
考点:利用导数研究函数的单调性,利用导数研究函数的极值
专题:导数的综合应用
分析:(Ⅰ)先求出函数的导数,得出m=1,于是f(x)在(0,+∞)单调递增,从而x=1不是f(x)的极小值点;
(Ⅱ)先求出函数的导数,分别讨论当m=0时,当0<m<1时,当m≥1时的情况,从而求出函数的单调递增区间;
(Ⅲ)先求出g(x)的表达式,得出g(x)≤g(1)恒成立;得不等式t2+(1+
m)t+
m-1≤0,解出即可.
(Ⅱ)先求出函数的导数,分别讨论当m=0时,当0<m<1时,当m≥1时的情况,从而求出函数的单调递增区间;
(Ⅲ)先求出g(x)的表达式,得出g(x)≤g(1)恒成立;得不等式t2+(1+
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:(Ⅰ)f′(x)=mx-2+
,
令f'(1)=0,得m=1;
当m=1时,f′(x)=
≥0,
于是f(x)在(0,+∞)单调递增,
∴x=1不是f(x)的极小值点;
(Ⅱ)f′(x)=
,
当m=0时,f(x)在(0,
)上单调递增;
当0<m<1时,f(x)在(0,
)上单调递增,(
,+∞)上单调递增;
当m≥1时,f(x)在(0,+∞)单调递;
(Ⅲ)g(x)=f(x)-lnx+x3=x3+
mx2-2x.
由题意,当x∈[1,t]时,g(x)≤g(1)恒成立;
易得g(x)-g(1)=(x-1)[x2+(1+
m)x+
m-1]≤0,
令h(x)=x2+(1+
m)x+
m-1,
因为h(x)必然在端点处取得最大值,即h(t)≤0,
即t2+(1+
m)t+
m-1≤0,
即
≥-2,解得,1<t≤
,
所以t的最大值为
.
| 1 |
| x |
令f'(1)=0,得m=1;
当m=1时,f′(x)=
| (x-1)2 |
| x+1 |
于是f(x)在(0,+∞)单调递增,
∴x=1不是f(x)的极小值点;
(Ⅱ)f′(x)=
| mx2-2x+1 |
| x |
当m=0时,f(x)在(0,
| 1 |
| 2 |
当0<m<1时,f(x)在(0,
1-
| ||
| m |
1+
| ||
| m |
当m≥1时,f(x)在(0,+∞)单调递;
(Ⅲ)g(x)=f(x)-lnx+x3=x3+
| 1 |
| 2 |
由题意,当x∈[1,t]时,g(x)≤g(1)恒成立;
易得g(x)-g(1)=(x-1)[x2+(1+
| 1 |
| 2 |
| 1 |
| 2 |
令h(x)=x2+(1+
| 1 |
| 2 |
| 1 |
| 2 |
因为h(x)必然在端点处取得最大值,即h(t)≤0,
即t2+(1+
| 1 |
| 2 |
| 1 |
| 2 |
即
| -t2-t+1 |
| t+1 |
1+
| ||
| 2 |
所以t的最大值为
1+
| ||
| 2 |
点评:本题考查了函数的单调性,函数的最值问题,考查导数的应用,求参数的范围,是一道综合题.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
设f0(x)=cosx,且对任意的n∈N,都有 fn+1(x)=fn′(x),则f2013(x)=( )
| A、cosx | B、sinx |
| C、-sinx | D、-cosx |
如图给出的是计算
+
+
+…+
的值的一个程序框图,判断其中框内应填入的条件是( )

| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 20 |

| A、i>10 | B、i<10 |
| C、i>20 | D、i<20 |
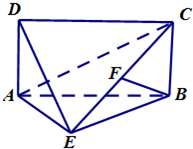 如图,四棱锥E-ABCD中,ABCD是矩形,平面EAB⊥平面ABCD,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE.
如图,四棱锥E-ABCD中,ABCD是矩形,平面EAB⊥平面ABCD,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE.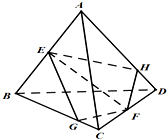 如图,在四面体ABCD中,E,F分别为AB,CD的中点,过EF任作一个平面
如图,在四面体ABCD中,E,F分别为AB,CD的中点,过EF任作一个平面