题目内容
已知函数f（x）=x3+（a+1）x2+（a+1）x+a，在其定义域内既有极大值又有极小值，则实数a的取值范围是（ ）
| A、-1＜a＜2 |
| B、a＞2或a＜-1 |
| C、a＜-1 |
| D、a＞2 |
考点：利用导数研究函数的极值
专题：导数的综合应用
分析：函数f（x）在R上既有极大值又有极小值，说明其图象先增后减再增，等价于其导函数有两个不相等的零点，即△＞0．
解答：
解：函数f（x）的定义域为R，f′（x）=3x2+2（a+1）x+a+1，
∵f（x）在其定义域内既有极大值又胡极小值，∴3x2+2（a+1）x+（a+1）=0有两个不相等的实数根，
∴△=4（a+1）2-12（a+1）＞0解得：a＜-1或a＞2．
故选择：B．
∵f（x）在其定义域内既有极大值又胡极小值，∴3x2+2（a+1）x+（a+1）=0有两个不相等的实数根，
∴△=4（a+1）2-12（a+1）＞0解得：a＜-1或a＞2．
故选择：B．
点评：本题考查三次函数极值存在的条件，运用等价转化思想，属于基础题．
练习册系列答案
灵星计算小达人系列答案
孟建平错题本系列答案
相关题目
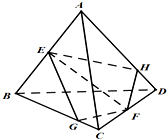如图，在四面体ABCD中，E，F分别为AB，CD的中点，过EF任作一个平面
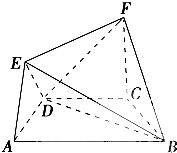在如图所示的几何体中，四边形ABCD是等腰梯形，AB∥CD，∠DAB=60°，FC⊥平面ABCD，AE⊥BD，CB=CD=CF=1，