题目内容

函数y=x2+2x在x=2处的切线的斜率为（　　）
A、2B、4C、8D、6
考点：利用导数研究曲线上某点切线方程
专题：
分析：求出原函数的导函数，求得f′（2）的值，即为函数y=x2+2x在x=2处的切线的斜率．
解答： 解：由f（x）=x2+2x，得f′（x）=2x+2，
∴f′（2）=6，
即函数f（x）=x2+2x在x=2处的切线的斜率为6．
故选：D．
点评：本题考查利用导数研究曲线上某点的切线方程，函数在x=x0处的导数，就是曲线上过点（x0，y0）的切线的斜率，是基础题．
练习册系列答案
相关题目
已知f（x）是定义在（0，+∞）上的非负可导函数，且满足xf′（x）-f（x）＞0，对任意正数a，b，若a＜b，则af（a），bf（b）的大小关系为（　　）
A、af（a）=bf（b）
B、af（a）＞bf（b）
C、af（a）≥bf（b）
D、af（a）＜bf（b）
若直线
x=1+2t
y=3+2t
（t为参数）与直线4x+ky=1垂直，则常数k=（　　）
A、7B、5C、4D、6
y=sin（3x-
π
6
）的单调递减区间是（　　）
A、[
2kπ
3
+
4π
9
，
2kπ
3
+
5π
9
]（k∈Z）
B、[
2kπ
3
+
2π
9
，
2kπ
3
+
5π
3
]（k∈Z）
C、[
2kπ
3
+
2π
3
，
2kπ
3
+
5π
3
]（k∈Z）
D、[
2kπ
3
+
2π
9
，
2kπ
3
+
5π
9
]（k∈Z）
在区间[0，3]上任取一个实数，则此实数小于1的概率为（　　）
A、
1
2
B、
1
3
C、
1
4
D、1
如图，Rt△ABC中，CD为斜边AB上的高，CD=6，且AD：BD=3：2，则斜边AB上的中线CE的长为（　　）
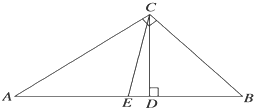
A、5
6
B、
5
6
2
C、
15
D、
3
10
2
已知数列{an}为等比数列，a4+a7=2，a5•a6=-8，则a1+a10的值为（　　）
A、7B、-5C、5D、-7
已知函数f（x）=x3+3mx2+nx+m2在x=-1时有极值为0，则m+n=（　　）
A、11B、4或11C、4D、8
函数y=sin（-x+
π
4
）在x∈[0，2π]的一个单调递增区间是（　　）
A、[0，
3π
4
]
B、[
π
4
，
3π
4
]
C、[
3π
4
，
7π
4
]
D、[
7π
4
，2π]

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网