题目内容
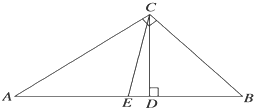
如图,Rt△ABC中,CD为斜边AB上的高,CD=6,且AD:BD=3:2,则斜边AB上的中线CE的长为( )

A、5
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:解三角形
专题:计算题,解三角形
分析:根据三角形相似,对应边成比例,列出AD、BD、CD的关系,根据关系式求出AB的长度,再利用直角三角形斜边上的中线等于斜边的一半,即可求出中线的长.
解答:
解:在Rt△ABC中
∵∠ACB=90°,CD⊥AB于D
∴△ACD∽△CBD
∴
=
∴CD2=AD•BD
又∵AD:BD=3:2
设AD=3x,则BD=2x
得3x•2x=36
解得x=
∴AB=5
又∵直角三角形斜边上的中线等于斜边的一半
∴CE=
AB=
.
故选:B.
∵∠ACB=90°,CD⊥AB于D
∴△ACD∽△CBD
∴
| CD |
| AD |
| BD |
| CD |
∴CD2=AD•BD
又∵AD:BD=3:2
设AD=3x,则BD=2x
得3x•2x=36
解得x=
| 6 |
∴AB=5
| 6 |
又∵直角三角形斜边上的中线等于斜边的一半
∴CE=
| 1 |
| 2 |
| 5 |
| 2 |
| 6 |
故选:B.
点评:本题通过三角形相似,对应边的比相等,求出斜边,再利用直角三角形斜边上的中线等于斜边的一半.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
△ABC的内角A、B、C的对边分别是a、b、c,且a2-c2+b2<0,则角C是( )
| A、小于600的角 |
| B、钝角 |
| C、锐角 |
| D、都有可能 |
设
,
分别是x轴,y轴正方向上的单位向量,
=3cosθ
+3sinθ
,θ∈(0,
),
=-
.若用α来表示
与
的夹角,则α等于( )
| i |
| j |
| OP |
| i |
| j |
| π |
| 2 |
| OQ |
| i |
| OP |
| OQ |
| A、θ | ||
B、
| ||
C、
| ||
| D、π-θ |
已知定点F(-a,0)(a>0),动点P在y轴上,M在x轴上,N为动点,且
•
=0,
+
=
,则动点N的轨迹为( )
| PM |
| PF |
| PM |
| PN |
| 0 |
| A、抛物线 | B、圆 | C、双曲线 | D、椭圆 |
函数y=x2+2x在x=2处的切线的斜率为( )
| A、2 | B、4 | C、8 | D、6 |
已f(x)为偶函数且
f(x)dx=8,则
f(x)dx等于( )
| ∫ | 6 0 |
| ∫ | 6 -6 |
| A、0 | B、4 | C、8 | D、16 |
函数y=|x+1|-2x零点的个数为( )
| A、0 | B、1 | C、2 | D、3 |
已知随机变量ξ服从二项分布,ξ~B(4,
),则P(ξ=1)的值为( )
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|