题目内容
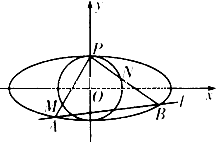 如图,椭圆C:
如图,椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| 4 |
| 5 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)求证△APB为直角三角形;
(Ⅲ)设直线MN的斜率为n,求证:
| m |
| n |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由椭圆C:
+
=1(a>b>0)的短轴长为2,解得b=1,由圆O将椭圆的长轴三等分,得a=3b=3,由此能求出椭圆C的方程.
(Ⅱ)由
,得(1+9m2)x2-
mx-
=0,由此推导出
•
=0,从而能证明△PAB为直角三角形.
(Ⅲ)设直线PA的斜率为k,k>0,则PA:y=kx+1,由
,得A(
,
),又直线l过点(0,-
),则m=
,由
,得M(
,
),MN过原点,n=kOM=
,由此能证明
为定值
.
| x2 |
| a2 |
| y2 |
| b2 |
(Ⅱ)由
|
| 72 |
| 5 |
| 81 |
| 25 |
| PA |
| PB |
(Ⅲ)设直线PA的斜率为k,k>0,则PA:y=kx+1,由
|
| -18k |
| 1+9k2 |
| 1-9k2 |
| 1+9k2 |
| 4 |
| 5 |
| k2-1 |
| 10k |
|
| -2k |
| 1+k2 |
| 1-k2 |
| 1+k2 |
| k2-1 |
| 2k |
| m |
| n |
| 1 |
| 5 |
解答:
(Ⅰ)解:∵椭圆C:
+
=1(a>b>0)的短轴长为2,∴2b=2,解得b=1,
∵圆O将椭圆的长轴三等分,∴2b=
×2a,
∴a=3b=3,
∴椭圆C的方程为
+y2=1.
(Ⅱ)证明:由
,消去y得(1+9m2)x2-
mx-
=0,
设A(x1,y1),B(x2,y2),则x1+x2=
,x1x2=
,
又P(0,1),∴
•
=(x1,y1-1)•(x2,y2-1)
=x1x2+(mx1-
)(mx2-
)
=x1x2+m2x1x2-
m(x1+x2)+
=(1+m2)•
-
m•
+
=
=0
∴PA⊥PB,∴△PAB为直角三角形.
(Ⅲ)证明:由(Ⅱ)知PA⊥PB,由题意知PA,PB的斜率存在且不为0,
设直线PA的斜率为k,k>0,则PA:y=kx+1,
由
,得
或
,
∴A(
,
),
又直线l过点(0,-
),
则m=
=
,
由
,得
,或
,
∴M(
,
),
又∵PM⊥PN,∴MN为⊙O的直径,∴MN过原点,∴n=kOM=
,
又∵m≠0,∴k2-1≠0,∴n≠0,
∴
=
=
,
∴
为定值
.
| x2 |
| a2 |
| y2 |
| b2 |
∵圆O将椭圆的长轴三等分,∴2b=
| 1 |
| 3 |
∴a=3b=3,
∴椭圆C的方程为
| x2 |
| 9 |
(Ⅱ)证明:由
|
| 72 |
| 5 |
| 81 |
| 25 |
设A(x1,y1),B(x2,y2),则x1+x2=
| 72m |
| 5(1+9m2) |
| -81 |
| 25(1+9m2) |
又P(0,1),∴
| PA |
| PB |
=x1x2+(mx1-
| 9 |
| 5 |
| 9 |
| 5 |
=x1x2+m2x1x2-
| 5 |
| 9 |
| 81 |
| 25 |
=(1+m2)•
| -81 |
| 25(1+9m2) |
| 9 |
| 5 |
| 72m |
| 5(1+9m2) |
| 81 |
| 25 |
=
| -18-81m2-648m2+81+81×9m2 |
| 25(1+9m2) |
∴PA⊥PB,∴△PAB为直角三角形.
(Ⅲ)证明:由(Ⅱ)知PA⊥PB,由题意知PA,PB的斜率存在且不为0,
设直线PA的斜率为k,k>0,则PA:y=kx+1,
由
|
|
|
∴A(
| -18k |
| 1+9k2 |
| 1-9k2 |
| 1+9k2 |
又直线l过点(0,-
| 4 |
| 5 |
则m=
| ||||
|
| k2-1 |
| 10k |
由
|
|
|
∴M(
| -2k |
| 1+k2 |
| 1-k2 |
| 1+k2 |
又∵PM⊥PN,∴MN为⊙O的直径,∴MN过原点,∴n=kOM=
| k2-1 |
| 2k |
又∵m≠0,∴k2-1≠0,∴n≠0,
∴
| m |
| n |
| ||
|
| 1 |
| 5 |
∴
| m |
| n |
| 1 |
| 5 |
点评:本题考查椭圆方程的求法,考查三角形为直角三角形的证明,考查两数比值为定值的证明,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
某校一社团共有10名成员,从周一到周五每天安排两人值日,若甲、乙必须排在同一天,且丙、丁不能排在同一天,则不同的安排方案共有( )
| A、21600 | B、10800 |
| C、7200 | D、5400 |
 己知函数f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)为奇函数,该函数的部分图象如图所示,△EFG是边长为2的等边三角形,则f(-1)的值为( )
己知函数f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)为奇函数,该函数的部分图象如图所示,△EFG是边长为2的等边三角形,则f(-1)的值为( )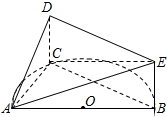 如图,AB是半圆O的直径,C是半圆O上除A、B外的一个动点,DC⊥平面ABC,DC∥BE,CD=BE,AB=4,tan∠EAB=
如图,AB是半圆O的直径,C是半圆O上除A、B外的一个动点,DC⊥平面ABC,DC∥BE,CD=BE,AB=4,tan∠EAB=
 如图,已知三棱柱ABC-A1B1C1中,D,E,F分别为AA1,CC1,AB的中点,M为BE的中点.求证:C1D∥平面B1FM.
如图,已知三棱柱ABC-A1B1C1中,D,E,F分别为AA1,CC1,AB的中点,M为BE的中点.求证:C1D∥平面B1FM.