题目内容

设函数f（x）=
ex-e-x
2
，g（x）=
ex+e-x
2
，求证：g（2x）=[g（x）]2+[f（x）]2．
考点：综合法与分析法(选修）
专题：函数的性质及应用
分析：直接代入方程的左侧与右侧化简证明即可．
解答： 证明：函数f（x）=
ex-e-x
2
，g（x）=
ex+e-x
2
，
所以g（2x）=
e2x+e-2x
2
，
[g（x）]2+[f（x）]2=[
ex+e-x
2
]2+[
ex-e-x
2
]2=
e2x+e-2x+2
4
+
e2x+e-2x-2
4
=
e2x+e-2x
2

∴g（2x）=[g（x）]2+[f（x）]2成立．
点评：本题考查指数函数的运算法则，等式的证明，考查计算能力．
练习册系列答案
相关题目
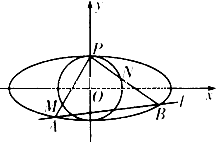如图，椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的短轴长为2，点P为上顶点，圆 O：x2+y2=b2将椭圆C的长轴三等分，直线l：y=mx-
4
5
（m≠0）与椭圆C交于A、B两点，PA、PB与圆O交于M、N两点．
（Ⅰ）求椭圆C的方程；
（Ⅱ）求证△APB为直角三角形；
（Ⅲ）设直线MN的斜率为n，求证：
m
n
为定值．
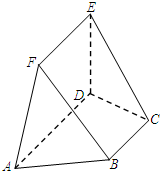如图，在五面体ABCDEF中，已知DE⊥平面ABCD，AD∥BC，∠BAD=60°AB=2，DE=EF=1．
（1）求证：BC∥EF；
（2）求三棱锥B-DEF的体积．
设数列{an}满足：a1=2，a2=8，an+2=（2+i2n）an+1+i2n，（i是虚数单位，n=1，2，3，…）．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）设数列{bn}满足bn=na2n，n∈N+，求数列{bn}的前n项和Tn．
已知全集U=R，集合A={x|1≤x≤2}，若B∪∁RA=R，B∩∁RA={x|0＜x＜1或2＜x＜3}，求集合B．
如图，已知正方体ABCD-A1B1C1D1的棱长为2，M为正方形AA1D1D的中心，N为棱AB的中点．
（Ⅰ）求证：MN∥平面BB1D1D；
（Ⅱ）求四棱锥N-BB1D1D的体积．
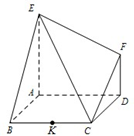如图，已知多面体EABCDF的底面ABCD是边长为2的正方形，EA⊥底面ABCD，FD∥EA，且FD=
1
2
EA=1．
（Ⅰ）求多面体EABCDF的体积；
（Ⅱ）求直线EB与平面ECF所成角的正弦值；
（Ⅲ）记线段BC的中点为K，在平面ABCD内过点K作一条直线与平面ECF平行，要求保留作图痕迹，但不要求证明．
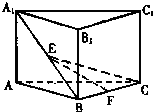如图，三棱柱ABC-A1B1 C1中，侧棱AA1⊥平面ABC，AB=BC=AA1=2，AC=2
2
，E，F分别是A1B，BC的中点．
（Ⅰ）证明：EF∥平面A AlClC；
（Ⅱ）证明：平面A1ABB1⊥平面BEC．
已知函数y=x-
x2-1
，求该函数的最大值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网