题目内容
 己知函数f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)为奇函数,该函数的部分图象如图所示,△EFG是边长为2的等边三角形,则f(-1)的值为( )
己知函数f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)为奇函数,该函数的部分图象如图所示,△EFG是边长为2的等边三角形,则f(-1)的值为( )A、-
| ||||
B、-
| ||||
C、
| ||||
D、-
|
考点:余弦函数的图象
专题:三角函数的图像与性质
分析:由函数的图象的顶点坐标求出A,由周期求出ω,由函数的奇偶性求出φ,可得函数的解析式,从而求得f(-1)的值.
解答:
解:由△EFG是边长为2的等边三角形,可得A=
,周期T=4=
,求得ω=
.
再根据函数f(x)=
cos(
x+φ)(0<φ<π)为奇函数,
可得φ=
,∴f(x)=-
sin
x,∴f(-1)=-
×(-1)=
,
故选:C.
| 3 |
| 2π |
| ω |
| π |
| 2 |
再根据函数f(x)=
| 3 |
| π |
| 2 |
可得φ=
| π |
| 2 |
| 3 |
| π |
| 2 |
| 3 |
| 3 |
故选:C.
点评:本题主要考查余弦函数的图象和性质,由函数y=Asin(ωx+φ)的部分图象求解析式,属于基础题.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
运行如图所示的程序,如果输出结果为sum=1320,那么判断框中应填( )


| A、i≥9 | B、i≥10 |
| C、i≤9 | D、i≤10 |
已知{an}是等比数列,a4•a7=-512,a3+a8=124,且公比为整数,则公比q为( )
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
y=cosx•sinx是( )
| A、奇函数 |
| B、偶函数 |
| C、既是奇函数也是偶函数 |
| D、既不是奇函数也不是偶函数 |
在极坐标系中,圆ρ=4cosθ的垂直于极轴的两条切线方程分别为( )
| A、θ=0(ρ∈R)和ρcosθ=4 | ||
B、θ=
| ||
| C、θ=0(ρ∈R)和ρcosθ=2 | ||
D、θ=
|
函数函数f(x)=x2-4x+5-2lnx的零点个数为( )
| A、3 | B、2 | C、1 | D、0 |
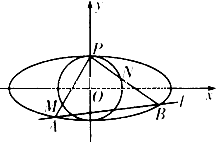 如图,椭圆C:
如图,椭圆C: