题目内容
 如图,已知三棱柱ABC-A1B1C1中,D,E,F分别为AA1,CC1,AB的中点,M为BE的中点.求证:C1D∥平面B1FM.
如图,已知三棱柱ABC-A1B1C1中,D,E,F分别为AA1,CC1,AB的中点,M为BE的中点.求证:C1D∥平面B1FM.考点:直线与平面平行的判定
专题:空间位置关系与距离
分析:连接AE,先证明出FM∥AE,进而证明出C1D∥AE,最后利用线面平行的判定定理证明出C1D∥平面B1FM.
解答:
证明:连接AE,
∵M,F为中点,
∴FM∥AE,
∵D,E为中点,
∴C1D∥AE,
∴FM∥C1D,
∵FM?平面B1FM,CD?平面B1FM,
∴C1D∥平面B1FM.
∵M,F为中点,
∴FM∥AE,
∵D,E为中点,
∴C1D∥AE,
∴FM∥C1D,
∵FM?平面B1FM,CD?平面B1FM,
∴C1D∥平面B1FM.
点评:本题主要考查了线面平行的判定定理的应用.证明的关键是找到或作出与平面中的线平行的线.

练习册系列答案
相关题目
已知{an}是等比数列,a4•a7=-512,a3+a8=124,且公比为整数,则公比q为( )
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
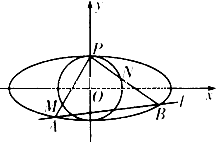 如图,椭圆C:
如图,椭圆C: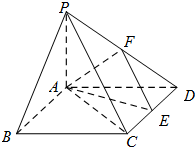 如图在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=
如图在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=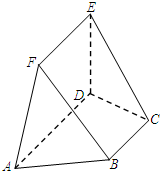 如图,在五面体ABCDEF中,已知DE⊥平面ABCD,AD∥BC,∠BAD=60°AB=2,DE=EF=1.
如图,在五面体ABCDEF中,已知DE⊥平面ABCD,AD∥BC,∠BAD=60°AB=2,DE=EF=1.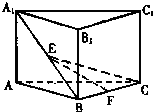 如图,三棱柱ABC-A1B1 C1中,侧棱AA1⊥平面ABC,AB=BC=AA1=2,AC=2
如图,三棱柱ABC-A1B1 C1中,侧棱AA1⊥平面ABC,AB=BC=AA1=2,AC=2